显示性偏好理论

出自 MBA智库百科(https://wiki.mbalib.com/)

显示性偏好理论（Revealed Preference Theory）、显示偏好理论

　　显示性偏好理论是由美国经济学家保罗·萨默尔森（P.Samuelson）提出来的，其基本精神是：消费者在一定价格条件下的购买行为暴露了或显示了他内在的偏好倾向。因此我们可以根据消费者的购买行为来推测消费者的偏好。这是一种不基于“偏好关系（效用函数）—消费者选择”的逻辑思路，而是一个相反的过程，即“消费者选择—偏好关系”。

　　该理论可以从消费者行为分辨最好的可能选择。换句话说，消费者的消费习惯可以显示他们的喜好。理论的出现，是基于消费者需求理论以边际替代率作为依归。而边际替代率的假设，就是消费者是为了把功用极大化而作消费决定。虽然公用极大化的假设不受争议，但需求理论隐含着的功用函数就难以被准确计算。显示性偏好理论就能弥补需求理论的不足，借观察行为来界定功用函数。

　　假设某甲有两个消费选择：买两个苹果和三条香蕉，或者买两条香蕉和三个苹果。如果两个选择的费用一样，而他选了前者，那就表示某甲喜欢前者多于后者。然后，这显示前者永远都较后者受欢迎。如果该消费者买后者，就一定是他负担不起买前者的费用。该理论进一步显示，偏好是带有传递关系的。如果我们有A、B、C 到 Z 多个选择，而偏好 A 多于 B 、 B 多于 C ，如此类推。那结论就显示出，我们对 A 的偏好多于 C ，一直数下去，多于 Z 。有了这套理论，经济学家就可以规划与消费者理论的模组一致的无差异曲线。

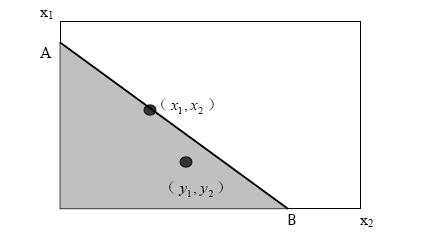
　　设消费者在价格为（p₁,p₂）时购买的商品束为（x₁,x₂），如果另一个商品组合（y₁,y₂）满足如下条件：

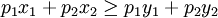　　 方程1

　　在这种情况下，若消费者总是在他能够购买的商品束中选择他最偏好的商品束，则一定有对（x₁,x₂）的偏好大于（y₁,y₂），即（x₁,x₂）是（y₁,y₂）的直接显示偏好。

　　1．间接显示性偏好

　　如果（x1,x2）是（y1,y2）的直接显示偏好，同时（y1,y2）是（z1,z2）的直接显示偏好，则（x1,x2）是（z1,z2）的间接显示偏好。

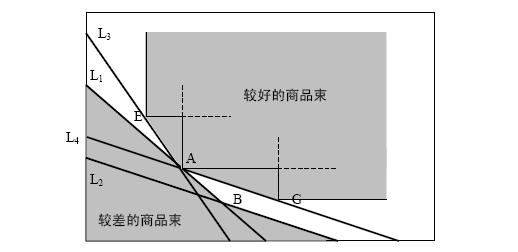
　　2.从显示性偏好到无差异曲线

　　　　图：无差异曲线的推导

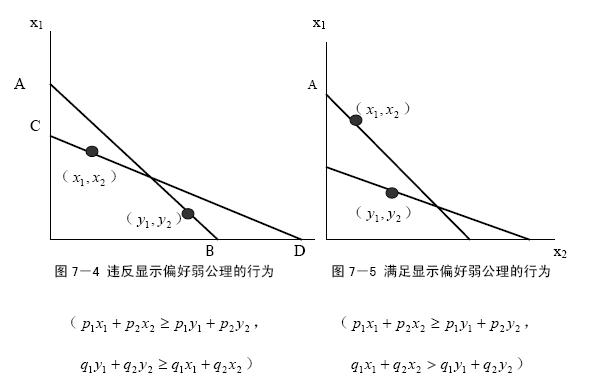
　　1.显示偏好弱公理（WARP）的含义：

　　如果（x1,x2）直接显示偏好于（y1,y2），且（x1,x2）和（y1,y2）是两个不同的商品束，则（y1,y2）就不可能直接显示偏好于（x1,x2）。

　　显示偏好弱公理表明：若消费者在价格（p1,p1）下选择（x1,x2），在价格（q1,q2）下选择（y1,y2），只要：

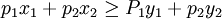　　 方程2

　　就不可能存在：

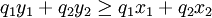　　 方程3

　　这意味着下式成立：

　　q₁x₁ + q₂x₂ > q₁y₁ + q₂y₂ 方程4

　　2．WARP的图示

　　3．WARP的检验：判断消费者的行为是否符合WARP

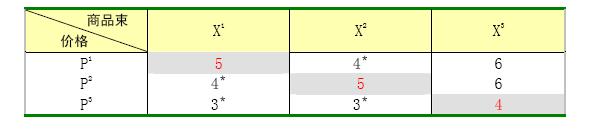
　　假设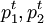（）表示第t期观察到的价格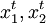，（）表示第t期观察到的消费者的选择，若我们对一个消费者的消费行为观察了3期，观察值如表1所示：

　　表1：消费者行为观察值

　　根据以上的观察值，我们可以判断该消费者的行为是否符合WARP。我们首先计算消费者在不同价格水平下，购买不同商品束所需要支付的货币，结果如表2所示：

　　对角线上的各个数据为消费者在三个观察期实际支出的费用，分别为：5，5，4。

　　在观察期1（t=1）,价格水平为p'＝(1，2)：消费者选择的商品束为X1（支出的货币额为5），由于此时商品束X2也是消费者能买得起的商品束（需要支付的货币为4），但是消费者没有购买，这表明商品束X¹ > X²，即：

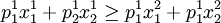　　 方程5

　　在观察期2（t=2），价格水平变为p2 ＝(2，1)，消费者选择的商品束变为X2（支付的货币额为5），但是此时商品束X1也是消费者所能够买得起的（需要支付的货币为4），而消费者没有购买此商品束，即：

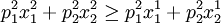　　 方程6

　　根据WARP可知，方程5和方程6不可能同时成立，因此该消费者的行为在X1与X2之间是不一致的，违背了WARP公理。

　　但是，该消费者在X3与X1及X2之间的，则没有违背WARP公理。

　　显示偏好强公理（SARP）是指如果（x1,x2）直接或间接显示偏好于（y1,y2），且（x1,x2）和（y1,y2）是两个不同的商品束，则（y1,y2）就不可能直接或间接显示偏好于（x1,x2）。

　　从西方经济学效用理论的发展中我们可以看到，序数效用论和显示偏好理论是在否定基数效用论的基础上发展起来的。从形式上看，这种否定确实避免了效用可以被直接计量这一令人困惑和尴尬的假设；但从内容上看，这种否定的有效性却非常值得怀疑。序数效用论和显示偏好理论对基数效用论的替代存在着明显的逻辑缺陷，主要表现在以下两个方面：

　　第一，序数效用论对基数效用论的替代是逻辑等价的同义反复。

　　我们知道，在序数效用论中无差异曲线凸向原点是一个未经证明的假定，而序数效用论的其他结论、包括边际替代率递减规律和切点定律都是从这一前提中推导出来的。事实上，从常规思维出发，我们也能发现破绽，一个可以排序（不论按什么标准）的事物却不能通过数量来进行描述，是一件很荒唐的事。由此可见，离开了基数，任何序数都不能得到完整的说明。多年来，西方经济学家仍不敢轻易抛弃基数效用论；才会出现我们前面提到的、在其他学科中绝无仅有的现象：两种矛盾的理论竟可以如此相安无事地和平共处。

　　第二，显示偏好理论是一个无法被经验反驳和证伪的循环论证。

　　我们在前面曾经提到，抛开繁复的数学证明，显示偏好理论无非要人们相信这样一个结论：消费者在市场上选择了某一消费品组合，他的偏好就同时被显示了，因此经济学家无需数量描述，就可以证明这一组合必然是效用最大化的。但是，用命题消费者选择的消费品必然是效用最大化的来证明命题消费者选择的是效用最大化的消费品，显然是一个逻辑上的循环论证。因为显示偏好理论事实上是用这样一种方法来证明消费者的理性行为：某个消费品只要被消费者选择了，那么它肯定就是效用最大化的。这一结论没有给经验判断留下丝毫反驳和证伪的余地！按照这个逻辑来推论，消费者在任何情况下都是理性的：不抽烟是理性的，抽烟也是理性的；不酗酒是理性的，酗酒也是理性的；甚至吸毒和自杀都可以被视作一种理性行为，因为这些行为都是一个人根据自身偏好最大化作出的选择。

　　批判理性主义哲学的创始人波普尔在批判弗洛伊德精神分析法的伪科学性质时曾经举过一个例子：任何可以想到的病例和行为都能用弗洛伊德的理论加以解释，例如，一个人为了淹死一个小孩而把他推入水中，另一个人为了拯救一个小孩而牺牲了自己的生命；按照弗洛伊德的理论，第一个人是因为恋母情结受到了压抑，第二个人是因为恋母情结得到了升华。波普尔说，一种在任何情况下都适用（尽管不排除在某些情况下它的确适用）并且总是得到证实的理论不可能是科学的理论，判别一种理论是否科学的标准不是它的可证实性，而是它的可证伪性；换言之，科学的理论不能一劳永逸地在肯定的意义上被选拔出来，而只能在否定的意义上借助经验检验被选拔出来。

　　在波普尔看来，一个经验的科学体系必须可以被经验所反驳，那些可以解释一切的理论，正是由于它们不可能被经验证伪而失去了作为科学理论的资格。特别值得指出的是，波普尔认为数学命题不是科学，因为它们与逻辑重言式一样均属于同义反复，且逻辑永真而不能被证伪!，因而不属于科学命题的范畴。

　　显示偏好理论把效用最大化能不能定量分析这样一个实证性的经验命题演绎成一个纯粹的数学命题，不但没有解决基数效用论与序数效用论之间的矛盾，反而因企图回避这一矛盾使自己陷入了更大的逻辑困境。