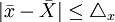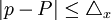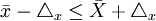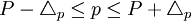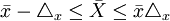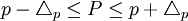抽样极限误差
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
抽样极限误差又称“置信区间和抽样允许误差范围”,是指在一定的把握程度(P)下保证样本指标与总体指标之间的抽样误差不超过某一给定的最大可能范围,记作Δ。
作为样本的随机变量——抽样指标值( 或p),是围绕以未知的唯一确定的全及指标真值(
或p),是围绕以未知的唯一确定的全及指标真值( 或P)为中心上下波动,它与全及指标值可能会产生正或负离差,这些离差均是抽样指标的随机变量,因而难以避免,只能将其控制在预先要求的误差范围(
或P)为中心上下波动,它与全及指标值可能会产生正或负离差,这些离差均是抽样指标的随机变量,因而难以避免,只能将其控制在预先要求的误差范围(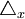 或
或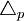 )内。
)内。
或
由于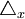 和
和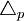 是预先给定的抽样方案中所允许的误差范围,所以利用
是预先给定的抽样方案中所允许的误差范围,所以利用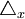 和
和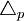 可以反过来估计未知的全及指标的取值可能的范围。解上述两个绝对值不等式便可得:
可以反过来估计未知的全及指标的取值可能的范围。解上述两个绝对值不等式便可得:
例1:例如要估计北京北站整车到达货物的平均运送时间。从交付的全部整车货票共26193批中,用不重复抽样抽取2718批货票。若允许的抽样极限误差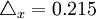 (天),经计算知所抽取的每批货物平均运送时间为
(天),经计算知所抽取的每批货物平均运送时间为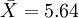 (天),那么北京北站整车到达货物的平均运送时间区间估计为(5.64-0.125,5.64+0.125),即在5.515到5.765天之间。
(天),那么北京北站整车到达货物的平均运送时间区间估计为(5.64-0.125,5.64+0.125),即在5.515到5.765天之间。
例2:资料同上,若要估计北京北站整车到达货物的逾期运到率(报告期内超过规定货物运到期限运到的货物批数/货物的到达总批数),从随机抽取的2718批货票中,计算得抽样逾期到率为6.43%,所确定的抽样极限误差为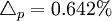 ,由此可得北京北站总体的逾期运到率的区间估计是(6.43%-0.642%,6.43%+0.642%)。
,由此可得北京北站总体的逾期运到率的区间估计是(6.43%-0.642%,6.43%+0.642%)。