平稳时间序列预测法
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
1、时间序列Yt取自某一个随机过程,如果此随机过程的随机特征不随时间变化,则称过程是平稳的;假如该随机过程的随机特征随时间变化,则称过程是非平稳的。
2、宽平稳时间序列的定义:设时间序列yt,对于任意的t,k和m,满足:
E(yt) = E(yt + m)
cov(yt,yt + k) = cov(yt + m,yt + m + k)
则称yt宽平稳。
3、Box-Jenkins方法是一种理论较为完善的统计预测方法。他们的工作为实际工作者提供了对时间序列进行分析、预测,以及对ARMA模型识别、估计和诊断的系统方法。使ARMA模型的建立有了一套完整、正规、结构化的建模方法,并且具有统计上的完善性和牢固的理论基础。
4、ARMA模型三种基本形式:自回归模型(AR:Auto-regressive),移动平均模型(MA:Moving-Average)和混合模型(ARMA:Auto-regressive Moving-Average)。
(1)自回归模型AR(p):如果时间序列yt满足
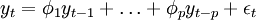
其中εt是独立同分布的随机变量序列,且满足:
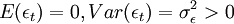
则称时间序列yt服从p阶自回归模型。或者记为φ(B)yt = yt − k。
平稳条件:滞后算子多项式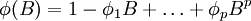 的根均在单位圆外,即φ(B) = 0的根大于1。
的根均在单位圆外,即φ(B) = 0的根大于1。
(2)移动平均模型MA(q):如果时间序列yt满足:
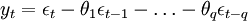
则称时间序列 服从q阶移动平均模型。或者记为yt = θ(B)ε1。
平稳条件:任何条件下都平稳。
(3)ARMA(p,q)模型:如果时间序列yt满足
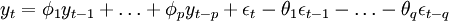
则称时间序列yt服从(p,q)阶自回归移动平均模型。或者记为φ(B)yt = θ(B)εt。
特殊情况:q=0,模型即为AR(p),p=0, 模型即为MA(q)。
1、自相关分析法是进行时间序列分析的有效方法,它简单易行、较为直观,根据绘制的自相关分析图和偏自相关分析图,我们可以初步地识别平稳序列的模型类型和模型阶数。利用自相关分析法可以测定时间序列的随机性和平稳性,以及时间序列的季节性。
2、自相关函数的定义:滞后期为k的自协方差函数为:rk = cov(yt − k,yt),则yt的自相关函数为: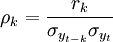 ,其中
,其中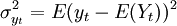 。当序列平稳时,自相关函数可写为:
。当序列平稳时,自相关函数可写为: 。
。
3、样本自相关函数为: ,其中
,其中 ,它可以说明不同时期的数据之间的相关程度,其取值范围在-1到1之间,值越接近于1,说明时间序列的自相关程度越高。
,它可以说明不同时期的数据之间的相关程度,其取值范围在-1到1之间,值越接近于1,说明时间序列的自相关程度越高。
4、样本的偏自相关函数:
5、时间序列的随机性,是指时间序列各项之间没有相关关系的特征。使用自相关分析图判断时间序列的随机性,一般给出如下准则:
①若时间序列的自相关函数基本上都落入置信区间,则该时间序列具有随机性;
②若较多自相关函数落在置信区间之外,则认为该时间序列不具有随机性。
6、判断时间序列是否平稳,是一项很重要的工作。运用自相关分析图判定时间序列平稳性的准则是:
①若时间序列的自相关函数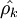 在k>3时都落入置信区间,且逐渐趋于零,则该时间序列具有平稳性;
在k>3时都落入置信区间,且逐渐趋于零,则该时间序列具有平稳性;
②若时间序列的自相关函数更多地落在置信区间外面,则该时间序列就不具有平稳性。
7、ARMA模型的自相关分析
AR(p)模型的偏自相关函数φkk是以p步截尾的,自相关函数拖尾。MA(q)模型的自相关函数具有q步截尾性,偏自相关函数拖尾。这两个性质可以分别用来识别自回归模型和移动平均模型的阶数。ARMA(p,q)模型的自相关函数和偏相关函数都是拖尾的。
1、单位根检验
①利用迪基—福勒检验(Dickey-Fuller Test)和菲利普斯—佩荣检验(Philips-Perron Test),也可以测定时间序列的随机性,这是在计量经济学中非常重要的两种单位根检验方法,与前者不同的事,后一个检验方法主要应用于一阶自回归模型的残差不是白噪声,而且存在自相关的情况。
②随机游动
如果在一个随机过程中,yt的每一次变化均来自于一个均值为零的独立同分布,即随机过程yt满足:
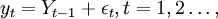
其中εt独立同分布,并且:

称这个随机过程是随机游动。它是一个非平稳过程。
③单位根过程
设随机过程yt满足: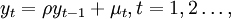 其中ρ = 1,μt为一个平稳过程并且
其中ρ = 1,μt为一个平稳过程并且
2、协整关系
如果两个或多个非平稳的时间序列,其某个现性组合后的序列呈平稳性,这样的时间序列间就被称为有协整关系存在。这是一个很重要的概念,利用Engle-Granger两步协整检验法和Johansen协整检验法可以测定时间序列间的协整关系。
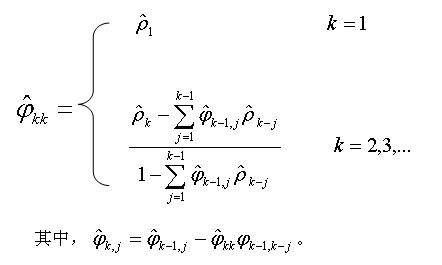








参考文献没有给出