无风险资产

出自 MBA智库百科(https://wiki.mbalib.com/)

无风险资产(risk free asset)

　　无风险资产是指具有确定的收益率，并且不存在违约风险的资产。

　　从数理统计的角度看，无风险资产是指投资收益的方差或标准差为零的资产。当然，无风险资产的收益率与风险资产的收益率之间的协方差及相关系数也为零。

　　从理论上看，只有由中央政府发行的、期限与投资者的投资期长度相匹配的、完全指数化的债券才可视作无风险资产。在现实经济中，完全符合上述条件的流通中的有价证券非常少。故在投资实务中，一般把无风险资产看作是货币市场工具，如国库券利率LIBOR。

　　(一) 不进行无风险借款时的投资组合

　　(1).投资于一种风险资产与一种无风险资产的组合

　　设某投资组合包含一种无风险资产（如无风险贷款）和一种风险资产。无风险资产的收益率为r_f，标准差为σ_f。风险资产的期望收益率为E(r_i)，标准差为σ_i，它在投资组合中所占的比重为w_i。风险资产与无风险资产的协方差为σ_if，相关系数为ρ_if。那么，该投资组合的期望收益率和方差分别为：

E(r_p) = w_iE(r_i) + (1 − w_i)E(rf)

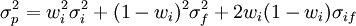
　　由于r_f为常数，σ_f = 0，且σ_if = E[r_i − E(r_i)][r_f − e(rf)] = 0，故：

E(r_p) = w_iE(r_i) + (1 − w_i)r_f

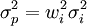
σ_p = w_iσ_i

将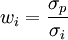代入E(r_p)的计算公式，可得：

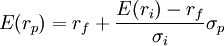
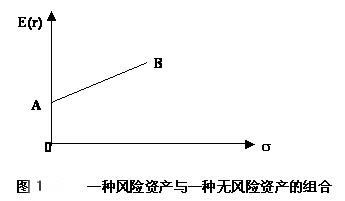
　　在上式中，r_f、E(r_i)和σ_i都已知。这说明，此时投资组合的期望收益率E(r_p)与其标准差σ_p之间呈线性关系。由于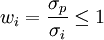，而且正常情况下风险资产的期望收益率E(r_i)应高于无风险资产的收益率r_f，因此，改变组合中风险资产和无风险资产的比例，按不同比例搭配构成的投资组合的集合将是如图1中的一条向上倾斜的直线段AB。

　　其中，A点表示组合中仅有无风险资产，A点的坐标为（0，r_f）。B点表示组合中仅有某种风险资产，B点的坐标为（σ_i，E(r_i)）。显然，直线段AB上所有的投资组合都是有效的，直线段AB就是由一种风险资产和一种无风险资产构成的投资组合的有效界面。

　　(2).投资于多种风险资产与一种无风险资产的组合

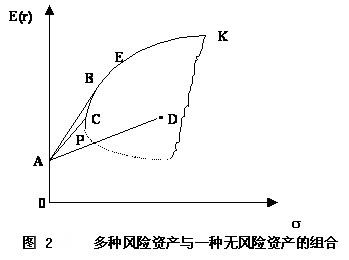
　　为简化问题，现在我们设想其中的每一个组合都被固定了下来。显然，这时集合中的每一个组合都相当于（或可以看作）一种期望收益率为E(r_i)、标准差为σ_i的风险资产。如果用其中的某一个组合和收益率为r_f的无风险资产按不同的比例构成一个新的投资组合的集合，那么这个新的投资组合的集合仍可以用一条直线段来体现。如图2所示，点A表示无风险资产，点D 是由多种风险资产构成的任一投资组合，连接点A和点D的直线段AD就表示由这一风险资产组合和无风险资产按不同的比例构成的各种新投资组合的集合。

　　现在我们来分析一下，在引入无风险资产之后，由无风险资产和多种风险资产构成的投资组合（简称新投资组合）的有效界面与原来仅有风险资产时的情形有何不同。为此，在图2中，我们仍用一个区域来表示多种风险资产构成的所有投资组合，并用点P表示这些风险资产的收益—方差界面上方差最小的证券组合 MVP。显然，在这些风险资产的有效界面P-E-K上我们总可以找到一点B，使得连接点A和点B的直线段AB刚好与风险资产的有效界面P-E-K相切于点 B。我们称点B所代表的投资组合为切点处的投资组合。它是风险资产的有效界面上一个非常特殊的投资组合。因为没有任何一种风险资产组合与无风险资产构成的新投资组合可以位于直线段AB的左上方，也就是说，直线段AB的斜率最大，直线段AB上的投资组合都是有效的。

　　与此相对应，另一个重要的事实是，在风险资产的有效界面P-E-K上，点B左下边的点所对应的投资组合不再是有效的。换句话说，曲线段P-C-B不再是新投资组合的有效界面的一部分。这是因为，对于曲线段P-C-B上的风险资产的任一有效组合而言，在期望收益率相等的情况下总可以在直线段AB上找到风险更小的投资组合；在风险相同的情况下也总可以在直线段AB上找到期望收益率更高的投资组合。于是，按照有效界面的定义，曲线段P-C-B上的投资组合不再是有效投资组合，而直线段AB上的投资组合都是有效的。这说明，当投资者可以同时投资于无风险资产和多种风险资产时，新投资组合的有效界面将由直线段AB和曲线段B-E-K构成，其中直线段AB代表点A对应的无风险资产和点B对应的风险资产组合以各种比例结合所构成的各种有效投资组合，而曲线段B-E-K则代表点B的右上方完全由风险资产所构成的各种有效投资组合。

　　(二) 存在无风险借款时的投资组合

　　在现实生活中，投资者往往可以借入资金并将其用于购买风险资产。由于借款必须支付利息，而利率是已知的，在该借款本息偿还上不存在不确定性，因此，我们可以把这种借款称为无风险借款。为简化起见，我们假定投资者可以按相同的利率进行无风险借款。

　　(1).无风险借款并投资于一种风险资产的情形

　　为了考察存在无风险借款时投资组合的有效界面，我们需要对前面的推导过程作适当的扩展。为此，我们只需把无风险借款看成负的无风险资产即可。仍设投资组合中风险资产所占的比重为w_i，则无风险借款所占的比重为(1 − w_i)，并且w_i > 1，1 − w_i < 0。按照同样的推导过程，我们仍然可以推导出下式成立：

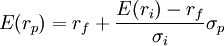
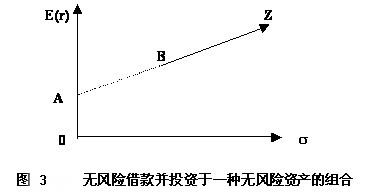
　　这说明，此时投资组合的期望收益率E(r_p)与其标准差σ_p之间仍然呈线性关系。然而，由于此时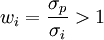，而且正常情况下风险资产的期望收益率E(r_i)应高于无风险借款的利率r_f，因此，此时投资组合的集合将表现为图1中直线段AB向右上方的延长线BZ（见图3）。显然，直线BZ上所有的投资组合都是有效的，直线BZ就是进行无风险借款并投资于一种风险资产时的有效界面。

　　(2).无风险借款并投资于多种风险资产的情形

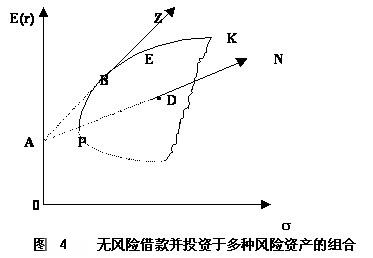
　　同样地，进行无风险借款并投资于多种风险资产的组合时，其风险和期望收益率的关系与投资于一种无风险资产和多种风险资产的组合相似。这时由多种风险资产构成的每一种组合仍相当于（或可以看作）一种期望收益率为E(r_i)、标准差为σ_i的风险资产。如果以无风险利率r_f进行无风险借款（相当于负的无风险投资）并将其投资于这种风险资产组合，那么随着无风险借款在组合中比例的改变，各种投资组合的集合表现为图2中连接点A和点D的直线段AD向右边的延长线DN（见图4）。其中，点A表示无风险借款，点D是由多种风险资产构成的任一投资组合。

　　现在我们来分析一下，在进行无风险借款并投资于多种风险资产的情形下，其有效界面与仅用期初的财富投资于多种风险资产时的情形有何不同。

　　为此，在图4中，我们仍用一个区域来表示多种风险资产构成的所有投资组合，并用点P表示这些风险资产的收益—方差界面上方差最小的证券组合MVP。

　　那么，在这些风险资产的有效界面P-E-K上我们仍可以找到一点B，使得连接点A和点B的直线段AB刚好与风险资产的有效界面P-E-K相切于点B。直线段AB向右上方的延长线BZ就表示进行无风险借款并投资于点B所对应的风险资产组合的各种可能组合。

　　由于直线BZ上的所有投资组合都优于曲线段B-E-K（风险资产有效界面上点B右上边的部分）上的投资组合，于是，按照有效界面的定义，此时曲线段 B-E-K上的投资组合不再是有效投资组合，而直线BZ上的投资组合都是有效的。这说明，当投资者可以进行无风险借款并投资于多种风险资产时，新投资组合的有效界面将由曲线段PB和直线BZ构成，其中曲线段PB代表点B的左下方完全由风险资产所构成的各种有效投资组合，直线BZ代表进行无风险借款并投资于点B对应的风险资产组合所构成的各种有效投资组合。

　　总之，综合上面的讨论，我们不难得出如下结论：如果同时存在无风险资产和风险资产可供投资者选择，同时又允许无风险借款，那么各种资产组合的有效界面将变成一条直线，该直线经过代表无风险资产的点A并与风险资产组合的有效界面相切。换句话说，它也就是图2中的直线段AB和图4中的直线BZ两者一起构成的射线A-B-Z。其中，点B为切点。

• 风险资产