信任博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
信任博弈(Trust Games)
目录 |
信任博弈实验最早由 Berg 、 Dickhaut 和 McCabe (1995)设计,此后 Fahr 和 Irlenbusch (2000)、Cox (2000)等进行了重复。
在该实验中,实验主持人首先支付给提议者一定数量x的钱,并要求提议者决定把其中的一部分y赠送给响应者,可以是0,也可以是全部x。然后,实验主持人把提议者赠送的钱乘以3倍后再交给响应者,这样响应者就得到了3y。提议者知道,如果自己赠送给响应者y,那么实验主持人将交给响应者3y。但是,响应者不知道,实验主持人会放大3倍,而认为是提议者赠送给自己3y。最后,响应者决定返还给提议者多少钱z,可以是0,也可以是全部3y。在纯粹自利偏好下,响应者不会返还任何数量的钱。而提议者知道响应者不会有任何返还,所以他也不会赠送任何数量的钱。但是,实际的博弈实验结果完全不是这样。提议者赠送了一定数量的钱,响应者也返还了一定数量的钱。并且,赠送数量和返还数量之间存在显著的正相关关系。
这与纯粹自利偏好的预测显著不同。一种解释就是响应者具有公平偏好。提议者赠送较多时其收益就会较低,实质是牺牲了自己的利益去增加响应者的利益。为了维护双方收益的公平,响应者会投桃报李,增加返还数量,以减少自己的收益,同时增加提议者的收益,从而提高双方之间收益分配的公平程度。而提议者知道响应者会以高返还回报高赠送,并且由于他知道实验主持人会把赠送数量扩大3倍,提议者会预期具有较强公平偏好的响应者提供的返还数量将大于自己的赠送数量(该实验事实上也证实人们的公平偏好相当强),所以他一开始就提供高赠送额。
礼物交换博弈实验和信任博弈实验的实验结果说明,个别具有公平偏好的行为人(比如,礼物交换博弈实验和信任博弈实验中的响应者)的公平性行为可能会主导其他人的自利性行为,而大大提高收益分配结果的公平程度,并且有可能帕累托改进社会福利(比如,在礼物交换博弈实验中,就是博弈双方都获得比纯粹自利偏好下更高的收益)。[1]
图解信任博弈[2]
本图集介绍了信任博弈实验是如何操作的。
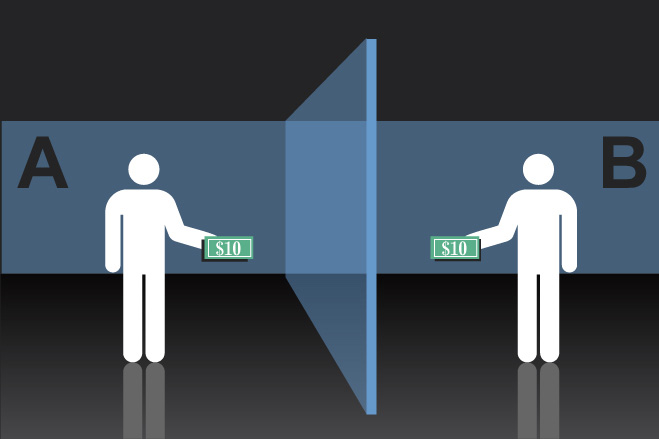
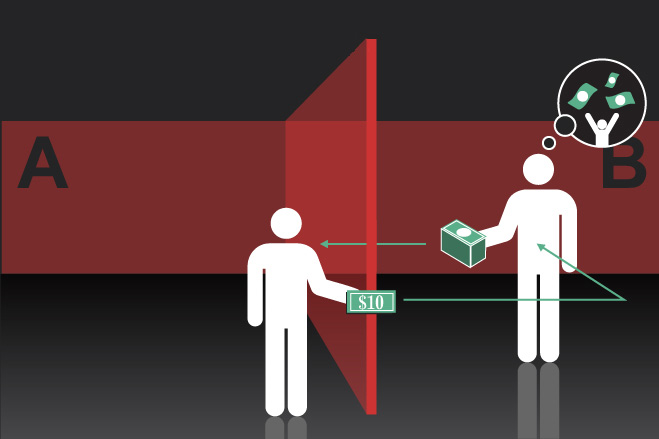
一、参与者(通常一次为16人)被分成A、B两组。所有人被告知他们的账户上均有象征性的10美元。随后,计算机向A组参与者发出提示,询问他们是否愿意将10美元的一部分或全部转账给随机挑选出的B组的一位匿名成员。
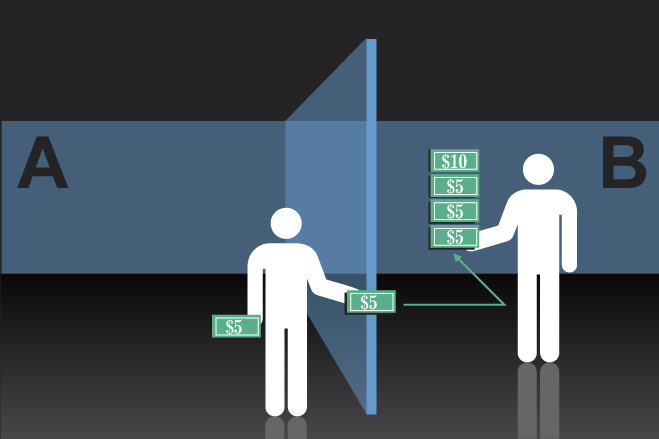
二、规则为无论A组成员转账多少,这笔钱到B组成员账户后都会变为原价值的三倍。90%的A组成员(信任者)都会给B组成员(接受者)转一些钱。
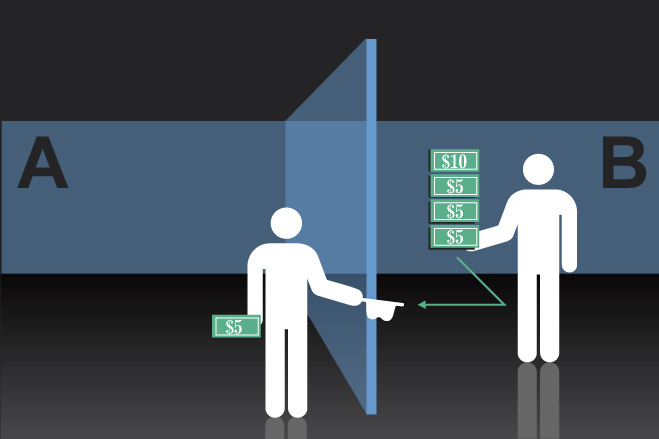
三、计算机会询问每位B组成员是否愿意将价值变为原先三倍的奖金回赠一部分给对应的A组成员。实验研究的问题是:A组成员是否信任B组成员会做出回报?(记住,这是在匿名条件下进行的。因此,没人会知道某位B组成员是否留下了所有钱。)
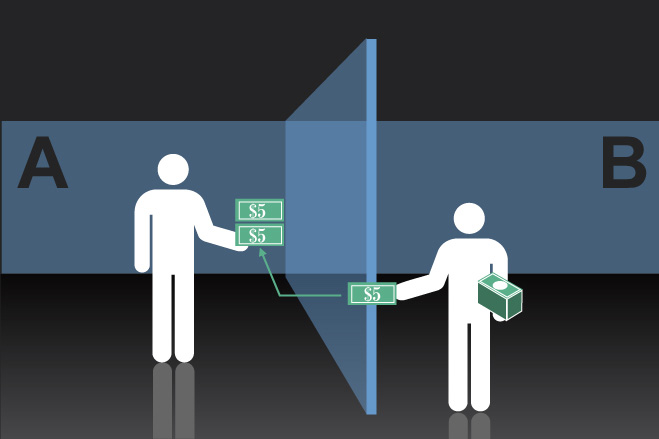
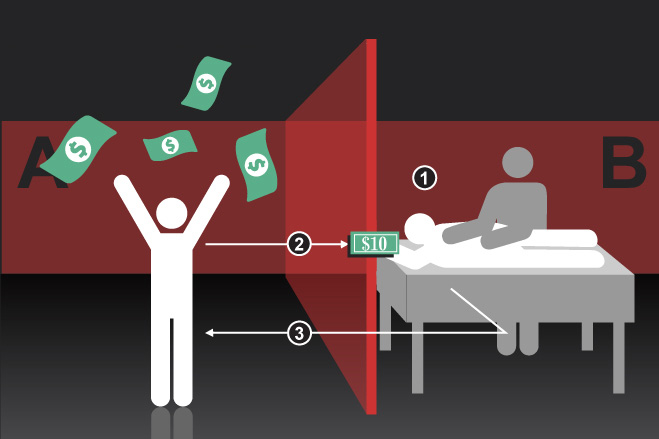
四、收到钱的B组成员中有95%的人会回赠一部分。最终,那些决定信任伙伴并将一部分钱转账的A组成员们平均有14美元,B组成员则平均有17美元。
五、所有参与者的血样。他们发现,感到被信任时,参与者的催产素会增加。A组成员送来的钱越多,相应的B组成员体内的催产素水平就越高;后者回赠给前者的钱也就越多。(当钱被计算机随机转入B组成员的账户时,催产素水平无变化。)
六、博弈开始前,接受按摩的参与者催产素水平较安静休息的对照组高9%。差异最为显著的是接受了按摩并收到转账的B组成员:收到那笔象征信任的钱后,他们回赠的钱的数额整整多了243%。
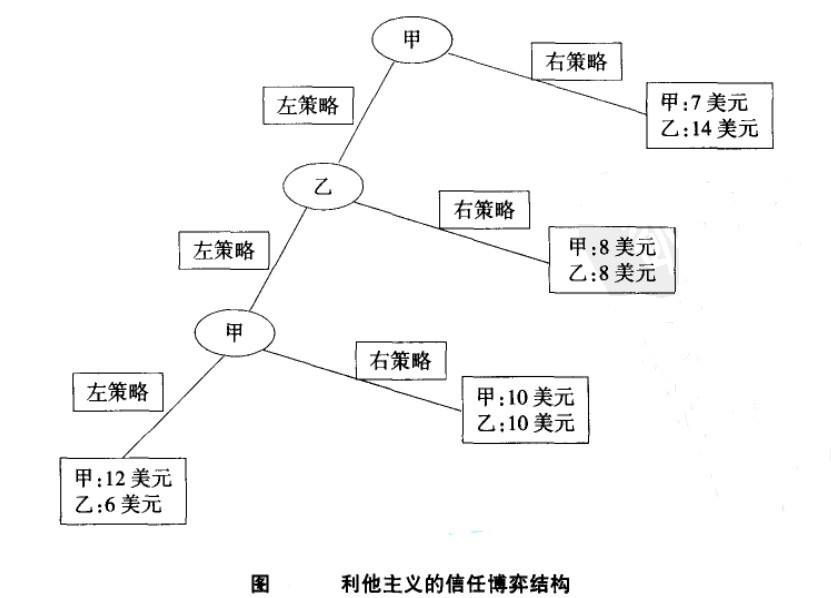
利他主义的信任博弈[3]
利他主义的信任博弈的结构可以参考图。首先是参与者甲采取行动,他可以采取右策略,结果博弈结束,甲得到7美元,乙得到14美元,也可以采取左策略,其未来的得益将取决于乙的后继选择。如果乙选择右策略,则每个参与者可以各得8美元,试验结束;如果乙选择左策略,则乙的得益取决于甲的后继选择。如果甲选择右策略,则每个参与者可以得到10美元,试验结束;如果甲选择左策略,则甲可以得到12美元,乙可以得到6美元。根据博弈论知识,该博弈的子博弈完美均衡为每一参与者得到8美元。
如果参与者甲具有利他主义的偏好,并且愿意承担某些成本来大幅度地增加参与者乙的报酬的话,那么甲应该一开始就选择右策略。这样,其自身的报酬为7美元,只比在子博弈完美均衡状态时的8美元少1美元,乙参与者则可以得到14美元,比在子博弈完美均衡状态时的8美元多6美元。因此,参与者甲可以通过自己损失1美元,而使参与者乙增加6美元的报酬。甲只需要略微偏好参与者乙的福利增长,就足以使其一开始就选择右策略。
- ↑ 魏光兴,蒲勇健.公平偏好下的报酬契约设计及应用研究.四川大学出版社,2007.12
- ↑ 图解信任博弈.华尔街日报.2012年05月16日
- ↑ 苏同华.行为金融学教程.中国金融出版社,2006年6月








对我有极大的帮助