多目标决策法
出自 MBA智库百科(https://wiki.mbalib.com/)
多目标决策法(Multi-objective decision-making method)
目录 |
多目标决策是对多个相互矛盾的目标进行科学、合理的选优,然后作出决策的理论和方法。它是20世纪70年代后迅速发展起来的管理科学的一个新的分支。多目标决策与只为了达到一个目标而从许多可行方案中选出最佳方案的一般决策有所不同。
多目标决策有各种各样的形式,但其基本特征有两点,这就是目标间的不可公度性和目标间的矛盾性。前者是指各目标间通常没有统一的度量标准,因而难于进行比较后者是指增加某一目标的利益,常常使另外的某-或某些目标变坏,因而通常不存在一般意义下的最优解。显然,多目标决策与单目标决策有着质的区别。[1]
从人们在多目标条件下合理进行决策的过程和机制从上分析,多目标决策的理论主要有:多目标决策过程的分析和描述;冲突性的分解和理想点转移的理论;多属性效用理论;需求的多重性和层次性理论等。它们是构成多目标决策分析方法的理论基础。
在多目标决策中,有一部分方案经比较后可以淘汰,称为劣解;但还有一批方案既不能淘汰,又不能互相比较,从多目标上考虑又都不是最优解,称为“非劣解”(或“有效解”、“帕累托解)。
在社会经济系统的研究控制过程中我们所面临的系统决策问题常常是多目标的,例如我们在研究生产过程的组织决策时,既要考虑生产系统的产量最大,又要使产品质量高,生产成本低等。这些目标之间相互作用和矛盾,使决策过程相当复杂使决策者常常很难轻易作出决策。这类具有多个目标的决策总是就是多目标决策。多目标决策方法现已广泛地应用于工艺过程、工艺设计、配方配比、水资源利用、环境、人口、教育、能源、企业高速武器系统设计和评价、经济管理等领域。在多目标决策实践中也应遵循一定的行为准则,主要包括:
(1)在满足决策需要的前提下,尽量减少目标个数。可采用剔除从属性目标,并把类似的目标合并为一个目标,或者把那些只要求达到起码标准而不要求达到最优的次要目标降为约束条件;以及通过同度量求和、求平均值或构成综合函数的方法,用综合指标来代替单项指标的办法达到目的。
(2)按照目标的轻重缓急,决定目标的取舍。为此,就要将目标按重要程度排列出一个顺序,并规定出重要性系数,以便在选优决策时有所遵循。
(3)对相互矛盾的目标,应以总目标为基准进行协调,力求对各目标全面考虑,统筹兼顾。
处理多目标决策问题,第一步就是找出非劣解,如果非劣解只有一个,就薛蹭为最优方案,如果不只一个,就无最优解,而需按一定法则从它们之中选出一个比较好的作为答案,这个解称为“较好解”。
这些概念用数学语言来描述,可以表示为:有 N个目标 ![f_1(X_i),f_2(X_i),f_3(X_i),\ldots,f_n(X_i)(X=[X_1,X_2,\ldots X_m])](/w/images/math/c/6/b/c6b41cffa7ebfbb79ce1783409c92d70.png) ,X是各函数中的变量,决策的目的是使各目标均取极大值,即
,X是各函数中的变量,决策的目的是使各目标均取极大值,即
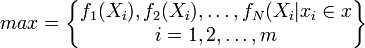 (x是 xi的集合)
(x是 xi的集合)
所谓这一问题的非劣解 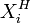 ,是指我们再也找不到一个或一组 Xi值,使得对所有的fi(Xi)[j=1,2,…N]来说,都有
,是指我们再也找不到一个或一组 Xi值,使得对所有的fi(Xi)[j=1,2,…N]来说,都有
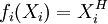
既然找不到一个或一组 Xi值能使
 ,则
,则 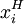 就是非劣解
就是非劣解
或
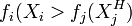
若另有一组 Xi值,使 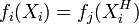 ,则这组 xi值亦为非劣解。
,则这组 xi值亦为非劣解。
这后一个条件是为了防止有两个目标值完全相同的非劣解时,将其中一个错判为劣解。
多目标决策的方法很多,有的要用线性规划、非线性规划、目标规划等方法。这里只介绍一下多目标决策中方案有限的几种方法。对于多目标的方案有限的决策问题一般先采用列表的方式。
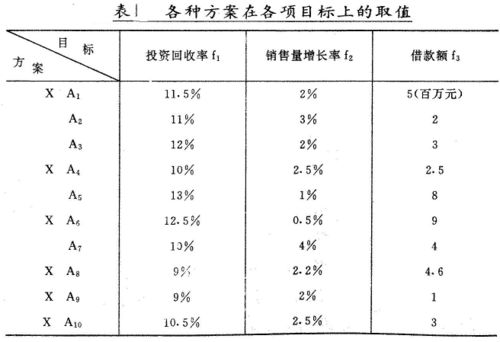
例,某厂要扩大生产,有 10个可行方案。考察各方案优劣的目标有投资回收率 f1,(越大越好),销售量的增长率f2(越大越好),借款额 f3(越低越好)。各种方案在各项目标上的取值情况见表1,要求找出非劣解,并从中选出一个“较好解”。
显然,从表中经过比较即可淘汰劣解,我们在劣解方案的在侧打上一个“X”号,例如 A1被 A3淘汰,A6被 A5淘汰等等,最后留下A2,A3,A5,A7,A9为非劣解。下一步从中选出“较好解”。
常用的方法有下述几种;
1.化多为少法。即将多目标改为由一个统一的综合目标来比较方案。包括综合评分法、平方和法及约束法。
2.目标分层法。把所有目标分别按其重要性排一个次序。
3.分层序列法:将所有目标按其重要性程度依次排序,先求出第一个最重要的目标的最优解,然后在保证前一目标最优解的前提下依次求下一目标的最优解,一直求到最后一个目标为止。
4.直接求非劣解法:先求出一组非劣解,然后按事先确定好的评价标准从中找出一个满意的解。
5.目标规划法:对于每一个目标都事先给定一个期望值,然后在满足系统一定约束条件下,找出与目标期望值最近的解。
6.多属性效用法:各个目标均用表示效用程度大小的效用函数表示,通过效用函数构成多目标的综合效用函数,以此来评价各个可行方案的优劣。
7.层次分析法:把目标体系结构予以展开,求得目标与决策方案的计量关系。
8.重排序法:把原来的不好比较的非劣解通过其他办法使其排出优劣次序来。
- ↑ 杨剑波. 多目标决策方法与应用[M]. 湖南出版社, 1996.








线性加权法、TOPSIS法和密切值法??