矩陣數據分析法

出自 MBA智库百科(https://wiki.mbalib.com/)

矩陣數據分析法（Matrix Data Analysis Chart）

　　矩陣數據分析法（Matrix Data Analysis Chart），它是新的質量管理七種工具之一。

　矩陣圖上各元素間的關係用數據進行量化，使整理和分析結果更加精確，這種用數據表示的矩陣圖法，叫做矩陣數據分析法。在QC新七種工具中，數據矩陣分析法是唯一種利用數據分析問題的方法，但其結果仍要以圖形表示。

　　數據矩陣分析法的主要方法為主成分分析法（Principal component analysis），利用此法可從原始數據獲得許多有益的情報。主成分分析法是一種將多個變數化為少數綜合變數的一種多元統計方法。

　　矩陣數據分析法，與矩陣圖法類似。它區別於矩陣圖法的是：不是在矩陣圖上填符號，而是填數據，形成一個分析數據的矩陣。

　　它是一種定量分析問題的方法。目前，在日本尚廣泛應用，只是作為一種“儲備工具”提出來的。應用這種方法，往往需求藉助電子電腦來求解。

　　在矩陣圖的基礎上，把各個因素分別放在行和列，然後在行和列的交叉點中用數量來描述這些因素之間的對比，再進行數量計算，定量分析，確定哪些因素相對比較重要的。

　　當我們進行顧客調查、產品設計或者其他各種方案選擇，做決策的時候，往往需要確定對幾種因素加以考慮，然後，針對這些因素要權衡其重要性，加以排隊，得出加權繫數。譬如，我們在做產品設計之前，向顧客調查對產品的要求。利用這個方法就能確定哪些因素是臨界質量特性。

　　1.可以利用親和圖（affinity diagram）把這些要求歸納成幾個主要的方面。然後，利用這裡介紹進行成對對比，再彙總統計，定量給每個方面進行重要性排隊。

　　2.過程決策圖執行時確定哪個決策合適時可以採用。

　　3.質量功能展開。兩者有差別的。本辦法是各個因素之間的相互對比，確定重要程度；而質量功能展開可以利用這個方法的結果。用來確定具體產品或者某個特性的重要程度。

　　當然，還有其他各種方法可以採用，但是，這種方法的好處之一是可以利用電子錶格軟體來進行。

　　下麵通過例子來介紹如何進行矩陣數據分析法。

　　1、確定需要分析的各個方面。我們通過親和圖得到以下幾個方面，需要確定它們相對的重要程度：易於控制、易於使用、網路性能、和其他軟體可以兼容、便於維護。

　　2、組成數據矩陣。用Excel或者手工做。把這些因素分別輸入表格的行和列，如表所示。

　　3、確定對比分數。自己和自己對比的地方都打0分。以 “行”為基礎，逐個和“列”對比，確定分數。“行”比“列”重要，給正分。分數範圍從9到1分。打1分表示兩個重要性相當。譬如，第2行“易於控制”分別和C列“易於使用”比較，重要一些，打4分。和D列“網路性能”比較，相當，打1分。…………如果“行”沒有“列””重要，給反過來重要分數的倒數。譬如，第3行的“易於使用”和B列的“易於控制”前面已經對比過了。前面是4分，現在取倒數，1/4=0.25。有D列“網路性能”比，沒有“網路性能”重要，反過來，“網路性能”比“易於使用”重要，打5分。現在取倒數，就是0.20。實際上，做的時候可以圍繞以0組成的對角線對稱填寫對比的結果就可以了。

　　表1：矩陣數據分析法

	A	B	C	D	E	F	G	H
1		易控制	易使用	網路性能	軟體兼容	便於維護	總分	權重%
2	易於控制	0	4	1	3	1	9	26.2
3	易於使用	0.25	0	0.20	0.33	0.25	1.03	3.0
4	網路性能	1	5	0	3	3	12	34.9
5	軟體兼容	0.33	3	0.33	0	0.33	4	11.6
6	便於維護	1	4	0.33	3	0	8.33	24.2
	總分之和	34.37

　　4、加總分。按照“行”把分數加起來。在G列內得到各行的“總分”。

　　5、算權重分。把各行的“總分”加起來，得到“總分之和”。再把每行“總分”除以“總分之和”得到H列每個“行”的權重分數。權重分數愈大，說明這個方面最重要，“網路性能”34.9分。其次是“易於控制”26.2分。

　　軟體缺陷的產生是由多方面的因素造成的，缺陷數據反映了開發過程中多個因素相互作用的對應關係。在實施了多個軟體項目的開發以後，已經積累了一定數量的歷史缺陷數據，我們如何利用這些數據找到開發過程中容易產生質量問題的環節和因素呢?如果只是粗略地看歷史統計數據，是很難看出各項目之間及項目的生命周期各階段的缺陷率的差異的。我們可以用這些歷史數據來設計一個矩陣，用矩陣數據分析法就能求出多個項目的各個階段產生缺陷率的高低，找到產生缺陷的關鍵因素，這樣可以幫助瞭解引入的缺陷，從而對新開發的項目會引入的缺陷數做出一個相當合理的預測，達到控制缺陷率，提高軟體質量的目的。隨著實施的軟體項目數量的增加，收集到的缺陷數據越來越多，生成的矩陣越大，對未來缺陷率預測和控制的準確性也就越高，軟體整體質量呈螺旋式穩步上升。

　　下麵通過一個例子來說明矩陣數據分析法在軟體缺陷管理中的具體應用。為了確定軟體缺陷主要出現在項目生命周期六個階段中的哪幾個階段，我們對n個開發項目進行統計，每個項目計算六個階段的缺陷密度，為了驗證結果重覆性，又將這n個項目分為Ⅰ、Ⅱ兩組，每組n／2個項目，然後對數據求均值、標準差、相關係數、特征值、特征向量，得出三個主成分，也就確定了項目生命周期中出現大部分缺陷的幾個階段，為改進項目薄弱環節提供依據。詳細步驟如下：

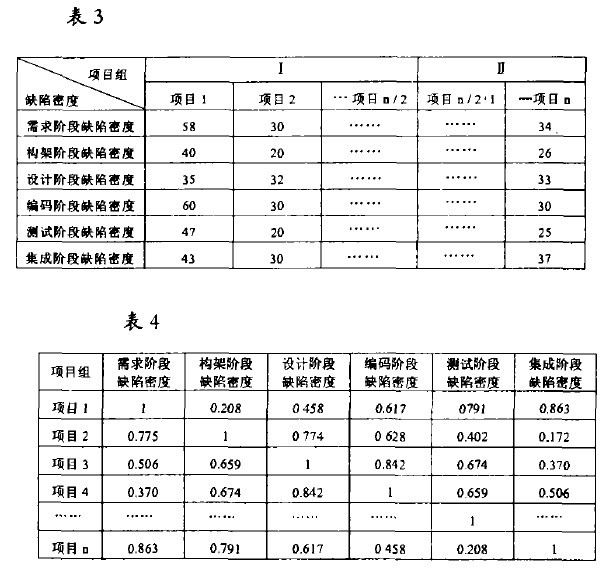
　　①將以往軟體項目積累的歷史缺陷數據進行分類、統計列表。各項目在生命周期各階段的歷史缺陷率數據見表3。

　　② 根據表3數據計算均值、標準差和相關係數，計算結果見表4。

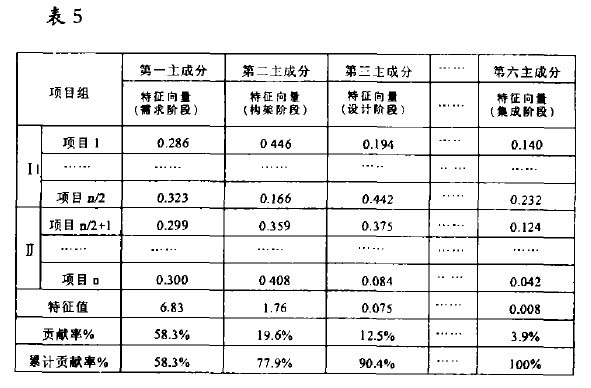
　　③根據相關係數矩陣(表4)求特征值、特征向量和貢獻率。由於計算量很大，方程的計算用電腦完成。計算結果見表5。

　　④ 分析計算結果。貢獻率代表主成分的影響程度，數值越大代表性越大，特征向量表示項目與該主成分的關係。從表5可看到，第一、二、三主成分的貢獻率達90．4％ ， 已代表所有變數的絕大部分，也就是說在項目開發過程中，軟體缺陷主要出現在項目生命周期的需求、構架和設計階段。這樣由上述的主成分分析，找到了容易出現軟體缺陷問題的階段，在以後的改進過程中把註意力集中到特征值大的方面來，就可以有效地控制、預防軟體缺陷問題。

• QC舊七大手法：管製圖、直方圖、散佈圖、因果圖、柏拉圖、檢查表、層別法。
• QC新七大手法：矩陣數據分析法、KJ法、關係圖法、矩陣圖法、系統圖法、PDPC法、箭形圖解法。