Tobit模型
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
Tobit模型也稱為樣本選擇模型、受限因變數模型,是因變數滿足某種約束條件下取值的模型。
這種模型的特點在於模型包含兩個部分,一是表示約束條件的選擇方程模型;一種是滿足約束條件下的某連續變數方程模型。研究感興趣的往往是受限制的連續變數方程模型,但是由於因變數受到某種約束條件的制約,忽略某些不可度量(即:不是觀測值,而是通過模型計算得到的變數)的因素將導致受限因變數模型產生樣本選擇性偏差。兩部模型(two-part model)與Tobit模型有很大的相似之處,也是研究受限因變數問題的模型;但是這兩種模型在模型結構形式、估計方法、假設條件等方面也存在一定的區別。
Tobit模型的形式如下:
yi = α + βxi + υi (1)
其中υi為隨機誤差項,xi為定量解釋變數。yi為二元選擇變數。此模型由James Tobin 1958年提出,因此得名。如利息稅、機動車的費改稅問題等。設
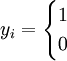
若是第一種選擇等於1,第二種選擇是0。
對yi取期望,
E(yi) = α + βxi (2)
下麵研究yi的分佈。因為yi只能取兩個值,0和1,所以yi服從兩點分佈。把yi的分佈記為,
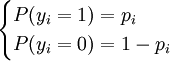
則:
E(yi) = 1(pi) + 0(1 − pi) = pi (3)
由(2)和(3)式有:
pi = α + βxi (yi的樣本值是0或1,而預測值是概率。) (4)
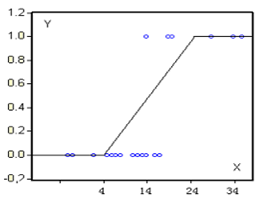
以pi = − 0.2 + 0.05xi 為例,說明xi 每增加一個單位,則採用第一種選擇的概率增加0.05。假設用這個模型進行預測,當預測值落在 [0,1] 區間之內(即xi取值在[4, 24] 之內)時,則沒有什麼問題;但當預測值落在[0,1] 區間之外時,則會暴露出該模型的嚴重缺點。因為概率的取值範圍是 [0,1],所以此時必須強令預測值(概率值)相應等於0或1(見下圖)。線性概率模型常寫成如下形式,
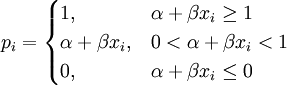 (5)
(5)
然而這樣做是有問題的。假設預測某個事件發生的概率等於1,但是實際中該事件可能根本不會發生。反之,預測某個事件發生的概率等於0,但是實際中該事件卻可能發生了。雖然估計過程是無偏的,但是由估計過程得出的預測結果卻是有偏的。
由於線性概率模型的上述缺點,希望能找到一種變換方法,(1)使解釋變數xi所對應的所有預測值(概率值)都落在(0,1)之間。(2)同時對於所有的xi,當xi增加時,希望yi也單調增加或單調減少。顯然累積概率分佈函數F(zi) 能滿足這樣的要求。採用累積正態概率分佈函數的模型稱作Probit模型。用正態分佈的累積概率作為Probit模型的預測概率。另外logistic函數也能滿足這樣的要求。採用logistic函數的模型稱作logit模型。
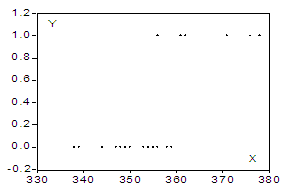
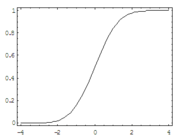
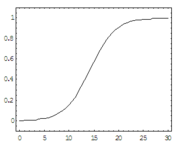








這個解釋是probit的模型。並不是Tobit