回歸直線法
出自 MBA智库百科(https://wiki.mbalib.com/)
回歸直線法(Linear Regression Method)
目錄 |
根據若幹期業務量和成本的歷史資料,運用最小平方法原理計算固定成本(或混合成本中的固定成本)和單位變動成本(或混合成本中變動部分的單位額)的一種成本性態分析方法。
回歸直線法的由來[1]
回歸直線法也稱直線回歸法,“回歸”名稱的由來歸功於英國統計學家高頓F·Glton(1822-1911)和他的學生皮爾森K·Pearson(1857-1936),他們在研究父母身高與其子女的遺傳問題時,發現高個子父輩的兒子們的平均高度要低於他們父輩的平均高度,矮個子父輩的兒子們的平均身高要高於他們父輩的平均身高,也就是說,沒有出現父輩個子高其兒子更高,父輩個子矮其兒子更矮的兩極分化現象,而都是朝標準身高(69.69inch)靠近)為了描述這種有趣的現象,高頓引進了“回歸”這個名詞來描述父輩身高x與子代身高y的這種直線關係:
y=33.73+0.516x
說明子代的身高朝著標準身高“回歸”,為了紀念高頓這個偉大的統計學家,以後被引申到把研究一個或一組非隨機變數來估計或預測某一個隨機變數的觀察值時,所建立的數學模型及所進行的統計分析,統稱為“回歸”分析。
如以業務量為自變數,成本為因變數,它們之間具有線性關係,則它們之間的關係可用下式表示:
y=a+bx
式中y代表總成本,a代表固定成本,b代表單位變動成本,x代表業務量。利用這個方程,就可認識和掌握成本在一定條件下的增減變動趨勢,公式為:
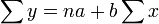
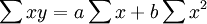
a,b的公式為:
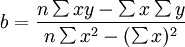
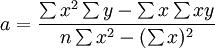
另外,求出b後,a還可以這樣求解
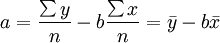
回歸直線的相關性檢驗[1]
根據回歸直線法,無論任何一組歷史數據資料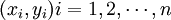 ,都可利用最小二乘法求得回歸直線
,都可利用最小二乘法求得回歸直線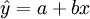 而不需要事先假定y與x具有線性相關關係,也就是說,雖然所求直線
而不需要事先假定y與x具有線性相關關係,也就是說,雖然所求直線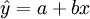 與其他所有直線相比,各點縱坐標
與其他所有直線相比,各點縱坐標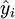 與歷史數據y_i之誤差平方和最小,但並不等於能很好地擬合歷史數據所確定的各個點(即x與y不一定相關),有時這種擬和甚至毫無意義,因此,必須進行相關性檢驗,所謂“相關性檢驗”,就是驗證所有的歷史數據
與歷史數據y_i之誤差平方和最小,但並不等於能很好地擬合歷史數據所確定的各個點(即x與y不一定相關),有時這種擬和甚至毫無意義,因此,必須進行相關性檢驗,所謂“相關性檢驗”,就是驗證所有的歷史數據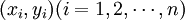 是否大致在一條直線上。
是否大致在一條直線上。
所採用的方法,有方差分析法和相關係數法,根據統計學原理,在概率為正態分佈的情況下,隨機變數出現在期望值±1個標準差範圍內的概率有68.26%,出現在期望值±2個標準差範圍內的概率有95.44%,出現在期望值±3個標準差範圍內的概率有99.72%(期望值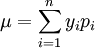 ,其中:p_i為第i個隨機變數的概率,標準差
,其中:p_i為第i個隨機變數的概率,標準差 )因此,隨機變數出現在期望值±3個標準差之外的概率為0.28%=0.0028,而單側概率只有0.14%=0.0014,我們不妨認為,實際值與期望值的最大誤差不超過±3個標準差,即實際值一般都在區間[μ − 3σ,μ + 3σ]上,為便於查表,取隨機變數出現在期望值±3個標準差之外的概率α = 0.005(α稱為顯著性水平或檢驗水平)。在此基礎上,介紹相關係數法和方差分析法。
)因此,隨機變數出現在期望值±3個標準差之外的概率為0.28%=0.0028,而單側概率只有0.14%=0.0014,我們不妨認為,實際值與期望值的最大誤差不超過±3個標準差,即實際值一般都在區間[μ − 3σ,μ + 3σ]上,為便於查表,取隨機變數出現在期望值±3個標準差之外的概率α = 0.005(α稱為顯著性水平或檢驗水平)。在此基礎上,介紹相關係數法和方差分析法。
- 1.相關係數法
相關係數法就是計算相關係數![r=\frac{n\sum^n_{i=1}x_i y_i-\sum^n_{i=1}x_i\sum^n_{i=1}y_i}{\sqrt{\left[n\sum^n_{i=1}x^2_i-(\sum^n_{i=1}x_i)^2\right]\left[n\sum^n_{i=1}y^2_i-(\sum^n_{i=1}y_i)^2\right]}}](/w/images/math/9/4/b/94bcad614b38e7d5747d61023759d3ac.png)
然後利用相關係數臨界值表查出r(α,n),若r > r(α,n),說明x與y存線上性關係,從而可建立直線方程y=a+bx,否則,說明x與y不存線上性關係,建立直線方程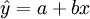 毫無意義。
毫無意義。
- 2.方差分析法
設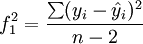
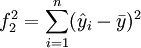
方差分析法就是計算
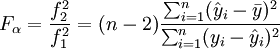
然後利用F分佈表查出Fα(1,n − 2)值,若Fα > Fα(1,n − 2),說明x與y存線上性關係,從而可建立直線方程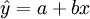 。
。
回歸直線的誤差估計[1]
誤差估計的方法很多,簡單的誤差估計有以下3種:
- 1.最大誤差法
最大誤差法是用歷史數據各期實際值與預測值誤差絕對值除以該期對應的自變數,取其最值,乘以預測期自變數,作為最大誤差的一種方法。
最大誤差=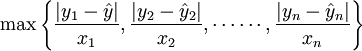
- 2.平均誤差法
平均誤差法是用距預測期最近的n期歷史數據中,每期實際值與預測值誤差的絕對值除以該期自變數,求和後乘 ,再乘預測期的自變數,作為估計誤差的一種方法。
,再乘預測期的自變數,作為估計誤差的一種方法。
- 3.標準差法
標準差法是用標準差與置信概率的關係來進行誤差估計的一種方法。
標準差=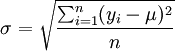
總之,回歸直線法的實質是以直線代替曲線,因此,不論在成本性態分析,還是在銷售預測、成本預測、利潤預測、資金預測以及其它方面,都必須進行相關性檢驗和誤差估計,否則,其結果就不可靠。
藉助於回歸直線法,可以使半變動成本的分解建立在科學分析和精確計算的基礎上。但計算工作量較大,比較麻煩。如能使用電子電腦計算,這種方法將會得到廣泛應用。







