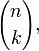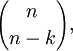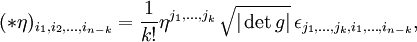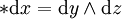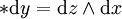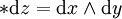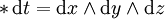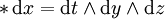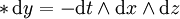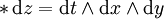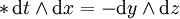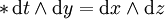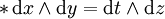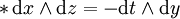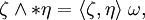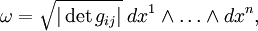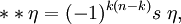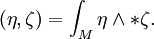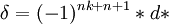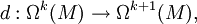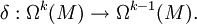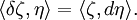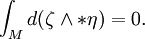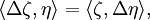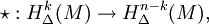霍奇對偶

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是霍奇對偶

　　霍奇對偶是指由蘇格蘭數學家威廉•霍奇引入的一個重要的線性映射。它定義在有限維定向 (數學)定向內積空間的外代數上。

[編輯]

霍奇對偶的維數與代數

　　霍奇星運算元在多重形式|k-形式空間與 (n -k)-形式空間建立了一個對應。一個 k-形式在這個對於下的像稱為這個 k-形式的霍奇對偶。k-形式空間的維數是

${n \choose k},\,$

　　後一個空間的維數是

${n \choose n - k},\,$

　　又由二項式繫數的對稱性，這兩個維數事實上相等。兩個具有相同維數的形式空間總同構；但不一定有一種自然或典範的方式。但霍奇對偶性利用了向量空間內積和定向，給出了一個特定的同構，因此在代數上這反應了二項式繫數的性質。這也在 k-形式空間上誘導了一個內積。“自然”定義意味著這個對偶性關係在理論中可起幾何作用。

　　第一個有趣的情形是在三維歐幾裡得空間 V。在這種情形，帕斯卡三角形相關行是

1, 3, 3, 1

　　霍奇對偶在兩個三維空間之間建立起一個同構，一個是 V 自己，另一個是 V 中兩個向量的楔積。具體細節參見#例子|例子一節。叉積只是三維的特殊性質，但霍奇對偶在所有維數都有效。

[編輯]

霍奇對偶的擴張

　　由於一個向量空間上 k 個變數的交錯線性形式空間自然同構於那個向量空間上的 k-向量空間的對偶空間|對偶，霍奇對偶也能對這些空間定義。與線性代數的大部分構造一樣，霍奇對偶可以擴張到一個向量叢。這樣的霍奇對偶特別常見的是在餘切叢的外代數（即流形上的微分形式）上，可用來從外導數構造餘微分，以及拉普拉斯-德拉姆運算元，它導致了緊黎曼流形上微分形式的霍奇分解。

[編輯]

k-向量的霍奇星號的正式定義

　　一個定向 (數學)|定向內積向量空間 V 上的霍奇星運算元是 V 的外代數上一個線性運算元，將 k-向量子空間與 (n-k)-向量自空間互換，這裡 n = dim V，0 ≤ k ≤ n。它具有如下性質，這些性質完全定義了霍奇星運算元：給定一個定向正交基 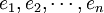$e_1,e_2,\cdots,e_n$ 我們有

$*(e_1\wedge e_2\wedge \cdots \wedge e_k)= e_{k+1}\wedge e_{k+2}\wedge \dots \wedge e_n.$

[編輯]

星運算元的指標記法

　　使用指標記法，霍奇對偶由張量縮並|縮並一個 k-形式與 n-維完全反對稱列維-奇維塔張量的指標得到。這不同於列維-奇維塔符號有一個額外因數 (det g)^½，這裡 g 是一個內積（如果 g 不是正定的，比如偽黎曼流形#洛倫茲流形|洛倫茲流形的切空間，則取行列式的絕對值）。

　　從而有

$(*\eta)_{i_1,i_2,\ldots,i_{n-k}}= \frac{1}{k!} \eta^{j_1,\ldots,j_k}\,\sqrt {|\det g|} \,\epsilon_{j_1,\ldots,j_k,i_1,\ldots,i_{n-k}},\,$

　　這裡 η 是任意一個反對稱 k 階張量。利用在定義列維-奇維塔張量中同一個內積 g 上升和下降指標。當然也可以對任何張量取星號，所得是反對稱的，因為張量的對稱分量在與完全反對稱列維-奇維塔張量縮並時完全抵消了。

[編輯]

霍奇對偶的例子

　　星運算元一個常見例子是在 n = 3，可以做為 3 維向量與斜對稱矩陣之間的對應。這不明顯地使用於向量分析中，例如由兩個向量的楔積產生叉積向量。具體地說，對歐幾裡得空間 R³，容易發現

$*\mathrm{d}x=\mathrm{d}y\wedge \mathrm{d}z$

和

$*\mathrm{d}y=\mathrm{d}z\wedge \mathrm{d}x$

以及

$*\mathrm{d}z=\mathrm{d}x\wedge \mathrm{d}y$

　　這裡 dx、dy 與 dz 是 R³ 上的標準正交微分1-形式。霍奇對偶在此情形顯然對應於三維中的叉積。

　　當 n = 4 時，霍奇對偶作用在第二外冪（6 維）上是自同態。它是一個對合，從而可以分解為子對偶與反自對偶子空間，在這兩個子空間上的作用分別為 +1 和 -1。

　　另一個有用的例子是 n = 4 閔可夫斯基時空，具有度量符號為 (+,-,-,-,) 與坐標 (t,x,y,z)，對1-形式有

$*\,\mathrm{d}t=\mathrm{d}x\wedge \mathrm{d}y \wedge\mathrm{d}z$

$*\,\mathrm{d}x=\mathrm{d}t\wedge \mathrm{d}y \wedge\mathrm{d}z$

$*\,\mathrm{d}y=-\mathrm{d}t\wedge \mathrm{d}x \wedge\mathrm{d}z$

$*\,\mathrm{d}z=\mathrm{d}t\wedge \mathrm{d}x \wedge\mathrm{d}y$

　　對2-形式有

$*\, \mathrm{d}t \wedge\mathrm{d}x = - \mathrm{d}y\wedge \mathrm{d}z$

$*\, \mathrm{d}t \wedge\mathrm{d}y = \mathrm{d}x\wedge \mathrm{d}z$

$*\, \mathrm{d}t \wedge\mathrm{d}z = - \mathrm{d}x\wedge \mathrm{d}y$

$*\, \mathrm{d}x \wedge\mathrm{d}y = \mathrm{d}t\wedge \mathrm{d}z$

$*\, \mathrm{d}x \wedge\mathrm{d}z = - \mathrm{d}t\wedge \mathrm{d}y$

$*\, \mathrm{d}y \wedge\mathrm{d}z = \mathrm{d}t\wedge \mathrm{d}x$

[編輯]

k-向量的內積

　　霍奇對偶在 k-向量空間上誘導了一個內積，即在 V 的外代數上。給定兩個 k-向量 $η$ 與 $ζ$ ，有

$\zeta\wedge *\eta = \langle\zeta, \eta \rangle\;\omega,\,$

這裡 ω 是正規化的體積形式。可以證明 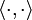$\langle\cdot,\cdot\rangle$ 是一個內積，它是半雙線性的，並定義了一個範數。反之，如果在 $Λ k (V)$ 上給了一個內積，則這個等式可以做為霍奇對偶的另一種定義^[1]。

　　本質上，V 的正交基元素的楔積組成了 V 的外代數的一個正交基。當霍奇星號擴張到流形上，可以證明體積形式能寫做

$\omega=\sqrt{|\det g_{ij}|}\;dx^1\wedge\ldots\wedge dx^n,\,$

　　其中 $g i j$ 是流形的度量張量|度量。

[編輯]

霍奇對偶的對偶性

　　當作用兩次時霍奇星號定義了一個對偶，不考慮符號的話，所得結果是外代數上一個恆等式。給定 n-維空間 V 上一個 k-向量 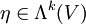$\eta \in \Lambda^k (V)$ ，我們有

$**\eta=(-1)^{k(n-k)}s\;\eta,\,$

　　這裡 s 與 V 上內積的度量符號|符號有關。具體說，s 是內積張量行列式的符號。例如，如果 n = 4 時，若內積的符號是 (+,-,-，-) 或 (-,+,+,+) 則 s = -1。對普通的歐幾裡得空間，符號總是正的，所以 s = +1。在普通向量空間，這一般不是一個問題。當霍奇星號擴張到偽-黎曼流形上時，上面的內積理解為對角形式的度量。

[編輯]