阿貝爾定理

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是阿貝爾定理

　　阿貝爾定理是指冪級數的一個重要結果。

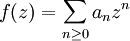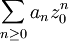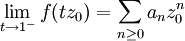　　設 $f(z)= \sum_{n \geq 0} a_n z^n$ 為一冪級數，其收斂半徑為R。若對收斂圓（模長為 R 的複數的集合）上的某個複數 $z 0$ ，級數 $\sum_{n\geq 0} a_n z_0^n$ 收斂，則有 $\lim_{t\to 1^-} f(t z_0) = \sum_{n \geq 0} a_n z_0^n$ 。

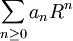　　若 $\sum_{n \geq 0} a_n R^n$ 收斂，則結果顯然成立，無須引用這定理。

[編輯]

阿貝爾定理的證明

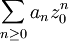　　設級數 $\sum_{n\geq 0} a_n z_0^n$ 收斂，下麵證明：

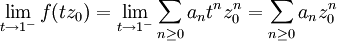
　　 $\lim_{t\to 1^-} f(t z_0) = \lim_{t\to 1^-} \sum_{n \geq 0} a_n t^n z_0^n = \sum_{n \geq 0} a_n z_0^n$

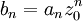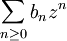　　令 $b_n = a_n z_0^n$ ，則冪級數 $\sum_{n\geq 0} b_n z^n$ 的收斂半徑為1，並且只需證明

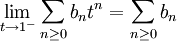
　　 $\lim_{t\to 1^-} \sum_{n \geq 0} b_n t^n = \sum_{n \geq 0} b_n$

　　令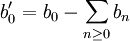 $b_0^{\prime} = b_0 - \sum_{n \geq 0} b_n$ ，則可化歸到 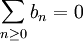$\sum_{n\geq 0} b_n =0$ ，於是以下只需要考慮 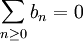$\sum_{n\geq 0} b_n =0$ 的情況。

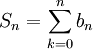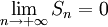　　設 $S_n = \sum_{k = 0}^n b_n$ ，那麼 $\lim_{n\to +\infty} S_n = 0$ 。由冪級數性質可知 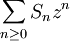$\sum_{n\geq 0} S_n z^n$ 的收斂半徑也是1。於是

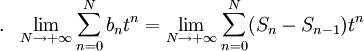
　　 $.\ \ \lim_{N\to +\infty} \sum_{n = 0}^N b_n t^n = \lim_{N\to +\infty} \sum_{n = 0}^N (S_n - S_{n-1}) t^n$

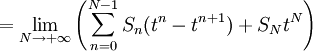
　　 $= \lim_{N\to +\infty} \left(\sum_{n = 0}^{N-1} S_n (t^n - t^{n+1}) + S_N t^N \right)$

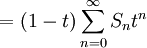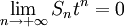　　 $= (1 - t) \sum_{n = 0}^{\infty} S_n t^n$ （因為 $\lim_{n\to +\infty} S_n t^n= 0$ ）

　　對於任意的 $ε > 0$ ，固定 $N 0$ 使得

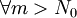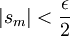
　　 $\forall m > N_0$ ， $|s_m|< \frac{\epsilon}{2}$

　　再固定 $δ$ 使得

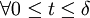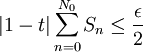
　　 $\forall 0 \le t \le \delta$ ， $|1 - t| \sum_{n = 0}^{N_0} S_n \le \frac{\epsilon}{2}$

　　於是對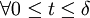 $\forall 0 \le t \le \delta$ ，

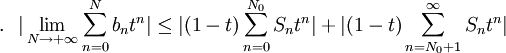
　　 $.\ \ | \lim_{N\to +\infty} \sum_{n = 0}^N b_n t^n | \le |(1 - t) \sum_{n = 0}^{N_0} S_n t^n | + |(1 - t) \sum_{n = N_0 + 1}^{\infty} S_n t^n |$

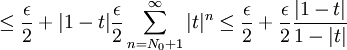
　　 $\le \frac{\epsilon}{2} + |1 - t| \frac{\epsilon}{2} \sum_{n = N_0 + 1}^{\infty} |t|^n \le \frac{\epsilon}{2} + \frac{\epsilon}{2} \frac{|1 - t|}{1 - |t|}$

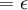
　　 $\displaystyle = \epsilon$

　　這就證明瞭

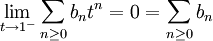
　　 $\lim_{t\to 1^-} \sum_{n \geq 0} b_n t^n = 0 = \sum_{n \geq 0} b_n$

　　於是阿貝爾定理得證。

　　從證明中可以看出，對於一個固定的正數 $α$ ，設區域：

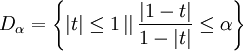
　　 $D_{\alpha} = \left\{ |t| \le 1 \left| \right| \frac{|1 - t|}{1 - |t|} \le \alpha \right\}$

　　那麼只要 $t$ 在 $D α$ 趨近於1，就有阿貝爾定理成立。

[編輯]

阿貝爾定理的例子和應用

　　阿貝爾定理的一個有用應用是計算已知收斂級數。方法是通過在級數每項後加上 $x n$ 項，將問題轉換為冪級數求和，最後再計算 x 趨於 1 時冪級數的極限。由阿貝爾定理可知，這個極限就是原級數的和。

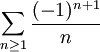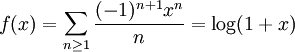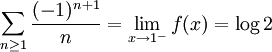
　　為計算收斂級數 $\sum_{n \geq 1} \frac{(-1)^{n+1}}{n}$ ，設 $f(x)= \sum_{n \geq 1} \frac{(-1)^{n+1} x^n}{n} = \log (1+x)$ 。於是有 $\sum_{n \geq 1} \frac{(-1)^{n+1}}{n} = \lim_{x \to 1^-} f(x) = \log 2$

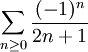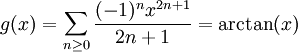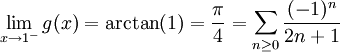
　　為計算收斂級數 $\sum_{n \geq 0} \frac{(-1)^n}{2n+1}$ ，設 $g(x)= \sum_{n \geq 0} \frac{(-1)^n x^{2n+1}}{2n+1} = \arctan (x)$ 。因此有 $\lim_{x \to 1^-} g(x) = \arctan (1) = \frac{\pi}{4} = \sum_{n \geq 0} \frac{(-1)^n}{2n+1}$

取自"https://wiki.mbalib.com/zh-tw/%E9%98%BF%E8%B4%9D%E5%B0%94%E5%AE%9A%E7%90%86"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

Tracy.

頁面分類: 數學定理

評論(共1條)

提示:評論內容為網友針對條目"阿貝爾定理"展開的討論，與本站觀點立場無關。

42.91.136.* 在 2021年9月24日 09:42 發表

123

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

阿貝爾定理

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是阿貝爾定理

阿貝爾定理的證明

阿貝爾定理的例子和應用

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共1條)

導航

意见反馈

查看

工具▼

阿貝爾定理

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是阿貝爾定理

阿貝爾定理的證明

阿貝爾定理的例子和應用

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共1條)

導航

意见反馈