里昂惕夫生產函數

出自 MBA智库百科(https://wiki.mbalib.com/)

　　里昂惕夫生產函數又稱固定投入比例生產函數，是指在每一個產量水平上任何一對要素投入量之間的比例都是固定的生產函數。假定生產過程中只使用勞動和資本兩種要素，則固定投入比例生產函數的通常形式為：

　　Q = Min(L/U，K/V)

　　其中，Q表示一種產品的產量，L和K分別表示勞動和資本的投入量，U和V分別表示為固定的勞動和資本的生產技術繫數，它們分別表示生產一單位產品所需要的固定的勞動投入量和資本投入量。該生產函數表示產量Q取決於兩個比值L/U和K/V中較小的那一個，即使其中的一個比例數值較大，也不會提高產量。在這裡，Q的生產被假定為必須按照L和K之間的固定比例，當一種生產要素的數量不能變動時，另一種生產要素的數量再多，也不能增加產量。需要指出的是，在該生產函數中，一般通常假定生產要素投入量L，K都滿足最小的要素投入組合的要求，所以有：

　　Q = L/U =K/V 即 K/L =V/U

　　上式清楚地體現了該生產函數的固定投入比例的性質，在這裡，它等於兩種要素的固定的生產技術繫數之比。對於一個固定投入比例生產函數來說，當產量發生變化時，各要素的投入量以相同的比例發生變化，所以，各要素的投入量之間的比例維持不變。關於固定投入比例生產函數的這一性質，可以用幾何圖形來說明。

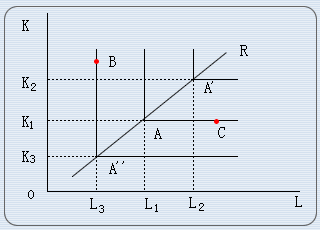
　　如上圖，橫軸和縱軸分別表示勞動和資本的投入數量，分別以A，A₁和A₂為頂點的三條含有直角的實線，順次表示生產既定的產量Q₁、Q₂和Q₃的各種要素組合。以生產Q₁的產量來說，A的要素組合（K₁，L₁）是生產產量Q₁的最小的要素投入量組合。以A點為頂點的兩條直角邊上的任何一點（不包括A點），都不是生產Q₁產量的最小的要素投入組合，例如，B點表示資本投入量過多，C點表示勞動投入量過多。如果產量由Q₁增加為Q₂，或由Q減少為Q₃，則最小要素投入組合相應地會由A點移至A₁點，或由A點移至A₂點。此時，兩要素投入量以相同的比例增減，兩要素投入比例保持不變，即：

　　K₁/L₁=K₂/L₂=K₃/L₃=V/U

　　因此，從原點出發經過A₂、A和A₁點的射線OR表示了這一固定比例生產函數的所有產量水平的最小要素投入量的組合。