車輛路徑問題
出自 MBA智库百科(https://wiki.mbalib.com/)
車輛路徑問題(Vehicle Routing Problem,VRP)
目錄 |
車輛路線問題(VRP)最早是由Dantzig和Ramser於1959年首次提出,它是指一定數量的客戶,各自有不同數量的貨物需求,配送中心向客戶提供貨物,由一個車隊負責分送貨物,組織適當的行車路線,目標是使得客戶的需求得到滿足,並能在一定的約束下,達到諸如路程最短、成本最小、耗費時間最少等目的[1]。
由此定義不難看出,旅行商問題(Traveling Saleman Problem,TSP)是VRP的特例,由於Gaery[2]已證明TSP問題是NP難題,因此,VRP也屬於NP難題。
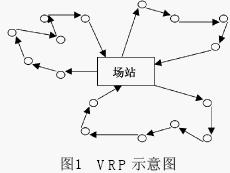
車輛路線問題自1959年提出以來,一直是網路優化問題中最基本的問題之一,由於其應用的廣泛性和經濟上的重大價值,一直受到國內外學者的廣泛關註。車輛路線問題可以描述如下(如圖1):
設有一場站(depot),共有M 輛貨車,車輛容量為Q,有N位顧客(customer),每位顧客有其需求量D。車輛從場站出發對客戶進行配送服務最後返回場站,要求所有顧客都被配送,每位顧客一次配送完成,且不能違反車輛容量的限制,目的是所有車輛路線的總距離最小。車輛路線的實際問題包括配送中心配送、公車路線制定、信件和報紙投遞、航空和鐵路時間表安排、工業廢品收集等。
車輛路徑問題的類型[3]
一般而言車輛路線問題大致可以分為以下三種類型(Ballou,1992):
1、相異的單一起點和單一終點。
2、相同的單一起點和終點。
3、多個起點和終點。
車輛路徑問題的方法[3]
關於車輛路線問題之學術研究文獻眾多,也提出了相當多的求解策略與方法,Bodin and Golden(1981)將眾多之求解方法歸納成以下七種:
- 數學解析法(Exact Procedure);
- 人機互動法(Interactive Optimization);
- 先分群再排路線(Cluster First–Route Second);
- 先排路線再分群(Route First–Cluster Second);
- 節省法或插入法(Saving or Insertion);
- 改善或交換法(Improvement or Exchanges);
- 數學規劃近似法(Mathematical programming)。
車輛路線問題研究現狀[4]
經過幾十年的研究發展,車輛路線問題研究取得了大量成果。下麵從車輛路線問題的現有研究型態和求解方法兩個方面介紹車輛路線問題的研究現狀。
在基本車輛路線問題(VRP)的基礎上,車輛路線問題在學術研究和實際應用上產生了許多不同的延伸和變化型態,包括時窗限制車輛路線問題(vehicle routing problems with time windows,VRPTW)、追求最佳服務時間的車輛路線問題(VRPDT)、多車種車輛路線問題(fleet size and mix vehicle routing problems,FSVRP)、車輛多次使用的車輛路線問題(vehicle routingproblems with multiple use of vehicle,VRPM)、考慮收集的車輛路線問題(vehicle routingproblems with backhauls,VRPB)、隨機需求車輛路線問題(vehicle routing problem with stochastic demand,VRPSD)等。
1、求解方法演進
綜合過去有關車輛路線問題的求解方法,可以分為精確演算法(exact algorithm)與啟髮式解法(heuristics),其中精密演算法有分支界限法、分支切割法、集合涵蓋法等;啟髮式解法有節約法、模擬退火法、確定性退火法、禁忌搜尋法、基因演算法、神經網路、螞蟻殖民演算法等。1995年,Fisher[5]曾將求解車輛路線問題的演算法分成三個階段。第一階段是從1960年到1970年,屬於簡單啟髮式方式,包括有各種局部改善啟髮式演算法和貪婪法(Greedy)等;第二階段是從1970年到1980年,屬於一種以數學規劃為主的啟髮式解法,包括指派法、集合分割法和集合涵蓋法;第三階段是從1990開始至今,屬於較新的方法,包括利用嚴謹啟髮式方法、人工智慧方法等。
2、啟髮式演算法
由於VRP是NP-hard問題,難以用精確算發求解,啟髮式演算法是求解車輛運輸問題的主要方法,多年來許多學者對車輛運輸問題進行了研究,提出了各種各樣的啟髮式方法。車輛運輸問題的啟髮式方法可以分為簡單啟髮式演算法、兩階段啟髮式演算法、人工智慧方法建立的啟髮式方法。
簡單啟髮式方法包括節省法或插入法、路線內/間節點交換法、貪婪法和局部搜索法等方法。節省法或插入法(savings or insertion)是在求解過程中使用節省成本最大的可行方式構造路線,直到無法節省為止。交換法則是依賴其他方法產生一個起始路線,然後以迭代的方式利用交換改善法減少路線距離,直到不能改善為止。1960年,Clarke和Wright[6]首先提出一種啟髮式節省法(savings methods)來建立車隊配送路線。簡單啟髮式方法簡單易懂、求解速度快,但只適合求解小型、簡單的VRP問題。
兩階段方法包括先分組後定路線(clusterfirst-route second)和先定路線後分組(routefirst-cluster second)兩種啟髮式策略。前者是先將所有需求點大略分為幾個組,然後再對各個組分別進行路線排序;後者則是先將所有的需求點建構成一條路線,再根據車輛的容量將這一路線分割成許多適合的單獨路線。
1990年以來,人工智慧方法在解決組合優化問題上顯示出強大功能,在各個領域得到充分應用,很多學者也將人工智慧引入車輛路線問題的求解中,並構造了大量的基於人工智慧的啟髮式演算法。禁忌搜索法(TS)基本上是屬於一種人工智慧型(AI)的局部搜尋方法,Willard首先將此演算法用來求解VRP ,隨後亦有許多位學者也發表了求解VRP的TS 演算法。西南交通大學的袁慶達[7]等設計了考慮時間視窗和不同車輛類型的禁忌演算法,這種演算法主要採用GENIUS方法產生初始解,然後禁忌演算法對初始解優化。模擬退火方法具有收斂速度快,全局搜索的特點,Osman[8]對VRP的模擬退火演算法進行了研究,他提出的模擬退火方法主要適合於解決路線分組。遺傳演算法具有求解組合優化問題的良好特性,Holland首先採用遺傳演算法(GA)編碼解決VRPTW 問題。現在多數學者採用混合策略,分別採用兩種人工智慧方法進行路線分組和路線優化。Ombuki[9]提出了用遺傳演算法進行路線分組,然後用禁忌搜索方法進行路線優化的混合演算法。Bent和Van Hentenryck[10]則首先用模擬退火演算法將車輛路線的數量最小化,然後用大鄰域搜索法(largneighborhood search)將運輸費用降到最低。
總結幾種人工智慧方法可以看出,TS演算法所得到的解最接近最優解,但其運算時間也最長,是GA演算法的2~3倍,SA演算法的近20倍;由於GA演算法也能較好的逼近最優解,同時使運算時間大大縮短,所以GA演算法能兼顧運算時間和效率兩方面,是具有較好的發展前途的方法;SA演算法求解速度非常快,也能提供一定程度上的優化方案在求解較小規模問題上具有較好效果。
- ↑ Paolo Toth,Daniele Vigo。THE VEHICLE ROUTING PROBLEM[M]。Society for Industrial and Applied Mathematics philadephia.2002
- ↑ 祝崇俊,劉民,吳澄.供應鏈中車輛路徑問題的研究進展及前景[J].電腦集成製造系統-CMS.2001,7(11):1-6
- ↑ 3.0 3.1 邱志鴻.物流配送中心貨車路線問題之研究
- ↑ 張強,荊剛,陳建嶺.車輛路線問題研究現狀及發展方向[J].交通科技,2004(1):60-62
- ↑ Fisher M L,Vehicle Routing.Handbooks in Operations Research & Management Science Vol 8,1995.1~33
- ↑ Clarke G,Wright J.Scheduling of vehicles from central depot to a number of delivery points[J].Operations Research,1964,12:568~581
- ↑ 袁慶達,閆昱,周再玲.Tabu Search演算法在優化配送路線問題中的應用.電腦工程,2001(11):86~89
- ↑ Osman I H.Meta-strategy simulated annealing an Tabu search algorithms for the vehicle routin problem.Annu Oper Res,1993,41:77~86
- ↑ Ombuki.B M,Nakamura M,Osamu M.Ahybri search based on genetic algorithm s and tabu search for vehicle routing.Brock University T echnica Report:#CS-02-07,2002,5:1~7
- ↑ R .Bent and P.Van Hentenryck.A two-stage hybri local search for the vehicle routing problem with tim windows.Technical Report,CS-01-06,Brown University,2001,9:1~30








good