解釋結構模型法

出自 MBA智库百科(https://wiki.mbalib.com/)

解釋結構模型法（Interpretative Structural Modelling Method,簡稱ISM方法）

　　解釋結構模型法是現代系統工程中廣泛應用的一種分析方法，是結構模型化技術的一種。它是將複雜的系統分解為若幹子系統要素，利用人們的實踐經驗和知識以及電腦的幫助，最終構成一個多級遞階的結構模型。此模型以定性分析為主，屬於概念模型，可以把模糊不清的思想、看法轉化為直觀的具有良好結構關係的模型。特別適用於變數眾多、關係複雜而結構不清晰的系統分析中，也可用於方案的排序等。它的應用面十分廣泛，從能源問題等國際性問題到地區經濟開發、企事業甚至個人範圍的問題等。

　　它在揭示系統結構，尤其是分析教學資源內容結構和進行學習資源設計與開發研究、教學過程模式的探索等方面具有十分重要作用，它也是教育技術學研究中的一種專門研究方法。

　　ISM的工作程式分為以下七步:

　　（1）實施ISM小組:一般由方法技術專家、協調人、參與者三方面人員組成;

　　（2）設定關鍵問題;

　　（3）選擇構成系統的影響關鍵問題的導致因素;

　　（4）列舉各導致因素的相關性;

　　（5）根據各要素的相關性，建立鄰接矩陣和可達矩陣;

　　（6）對可達矩陣分解後，建立結構模型;

　　（7）根據結構模型建立解釋結構模型。

　　ISM通過對錶示有向圖的相鄰矩陣的邏輯運算,得到可達性矩陣,然後分解可達性矩陣，最終使複雜系統分解成層次清晰的多級遞階形式。解釋結構模型在制訂企業計劃、城市規劃等領域已廣泛使用，尤其對於建立多目標、元素之間關係錯綜複雜的社會系統及其分析，效果更為顯著。

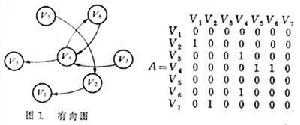
　　圖1:有向圖

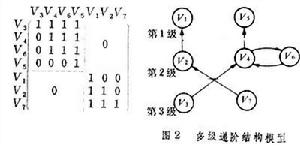
　　解釋結構模型用頂點V_i和V_j表示系統的元素(i=1,2,3…；j=1,2,3…)，帶箭頭的邊(V_i,V_j)表示兩元素之間的關係,即可構成有向圖（圖1）,用來表示有向圖中各元素間連接狀態的矩陣稱作相鄰矩陣A。當從V_i到V_j有帶箭頭的邊連接時,矩陣元素a_ij取值為1；無連接時取值為零。可達性矩陣M是用矩陣形式反映有向圖各頂點之間通過一定路徑可以到達的程度，它通過以下計算求得：將相鄰矩陣A加上單位矩陣I（矩陣中除主對角線上元素為1外，其餘元素皆為零的矩陣），然後用布爾代數規則 (0+0=0,0+1=1,1+1=1;0×0=0,0×1=0,1×1=1)進行乘方運算,直到兩個相鄰冪次方的矩陣相等為止。相等的矩陣中冪次最低的矩陣即為可達性矩陣。圖1所示有向圖的可達性矩陣M如下：通過對可達性矩陣的分解(有區域分解和級間分解)，即可建立系統的多級遞階結構模型（圖2）。

　　圖2:多級遞階結構模型

　　多級遞階結構模型非常直觀清楚地反映了該系統元素之間的結構關係。ISM方法使用方便,不需要高深的數學理論，易為系統分析人員所掌握。

　　案例：基於ISM法的太湖水華爆發要素分析

　　1.生成連接矩陣

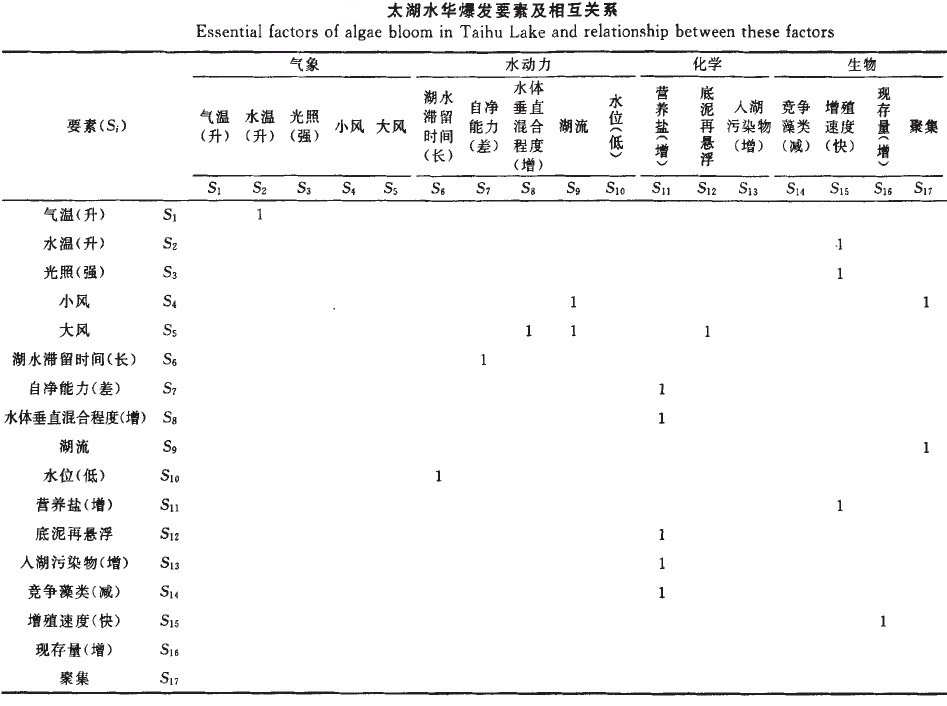
　　太湖水華爆發和許多因素有關，經過大量文獻資料檢索和分析，篩選出17個要素，並分析了各要素之間的關係，結果見表1。基於上表，得到連接矩陣A：

　　矩陣A

　　2.生成可達矩陣

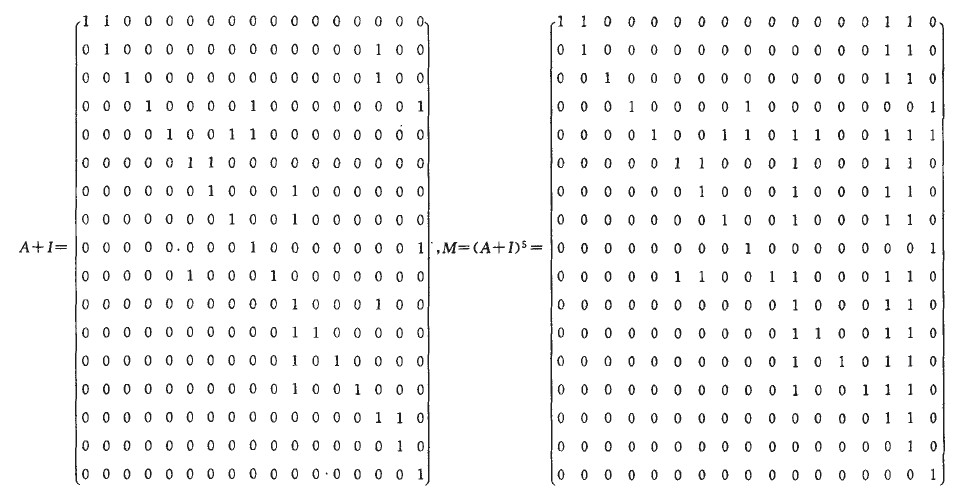
　　對矩陣(A+I)進行冪運算(基於布爾代數運算)，直至式(1)成立為止，通過計算求得，n=5和可達矩陣M = (A + J)⁵。

　　矩陣(A+I)

　　3.各要素的級別分配

　　根據可達矩陣M，求出各要素的可達集合P(S_i)、先行集合Q(S_i)，以及共同集合。滿足式(4)要求的有S₁₆、S₁₇由此確定第1級L₁ = S₁₆,S₁₇。其次，從可達矩陣M中刪除與要素S₁₆、S₁₇對應的第16行、第17行及第16列、第17列，得到矩陣M，在M上同理求出滿足式(4)的要素，得到第2級L₂ = S₉,S₁5，同理求得、、、。

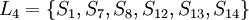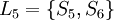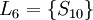　　矩陣M

　　17個要素分配在6個級別上，按這種級別順序排列矩陣M的行和列(不同級別間用虛線分塊划出，1‘表示有向枝連接相鄰級別間的要素)，得到：

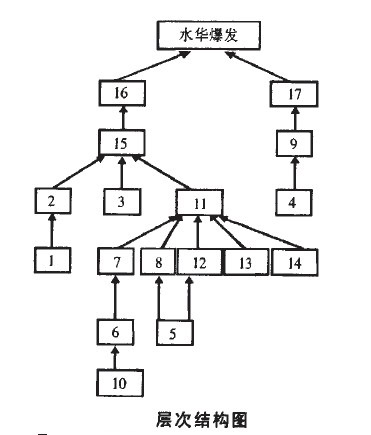
　　4.生成層次結構圖

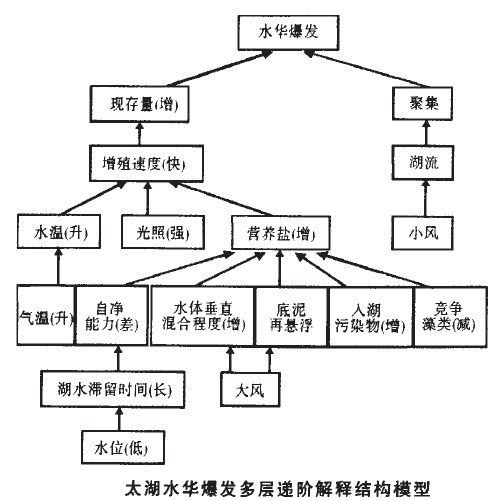
　　參照上述分塊三角化矩陣M，用有向枝連接相鄰級別間的要素(1‘部分)及同一級別的要素，可得到圖1所示的層次結構圖。通過圖1可以詳細分析各級別要素間的相互關係。將系統要素名稱填入層次結構圖，可得水華爆發的多層遞階解釋結構模型，結果見湖水華爆發多層遞階解釋結構模型。