線性插值法
出自 MBA智库百科(https://wiki.mbalib.com/)
線性插值法(linear interpolation)
目錄 |
什麼是線性插值法[1]
線性插值法是指使用連接兩個已知量的直線來確定在這兩個已知量之間的一個未知量的值的方法。
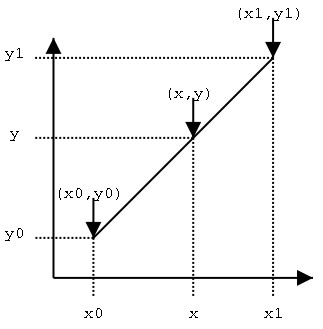
假設我們已知坐標(x0,y0)與(x1,y1),要得到[x0,x1]區間內某一位置x在直線上的值。根據圖中所示,我們得到兩點式直線方程:
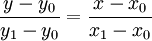
假設方程兩邊的值為α,那麼這個值就是插值繫數—從x0到x的距離與從x0到x1距離的比值。由於x值已知,所以可以從公式得到α的值
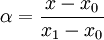
同樣,

這樣,在代數上就可以表示成為:
y = (1 − α)y0 + αy1
或者,
y = y0 + α(y1 − y0)
這樣通過α就可以直接得到 y。實際上,即使x不在x0到x1之間並且α也不是介於0到1之間,這個公式也是成立的。在這種情況下,這種方法叫作線性外插—參見 外插值。
已知y求x的過程與以上過程相同,只是x與y要進行交換。
線性插值經常用於已知函數f在兩點的值要近似獲得其它點數值的方法,這種近似方法的誤線定義為
RT = f(x) − ρ(x)
其中ρ表示上面定義的線性插值多項式

根據羅爾定理,我們可以證明:如果f有兩個連續導數,那麼誤差範圍是
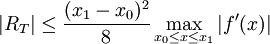
正如所看到的,函數上兩點之間的近似隨著所近似的函數的二階導數的增大而逐漸變差。從直觀上來看也是這樣:函數的曲率越大,簡單線性插值近似的誤差也越大。
線性插值法的計算實例[2]
線性插值法是認為現象的變化發展是線性的、均勻的,所以可利用兩點式的直線方程式進行線性插值。
兩點式的直線方程式為: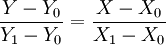 即
即 
式中 X0,Y0,X1,Y1——已知的統計數據;
X——X0,X1之間的任何數據;
Y——與X對應的插值數據。
例 某地區居民貨幣收入和消費支出情況如表1所示。試推算該地區居民收入為19.5億元時,其相應的消費支出是多少?
表1 居民貨幣收入和消費支出資料(單位:億元)
| 順序 | 貨幣收入(x) | 消費支出(y) |
| 0 | 18.2 | 15.8 |
| 1 | 19.8 | 17.2 |
解 
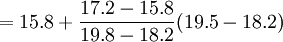
= 16.9
所以,當該地區居民收入是19.5億元時,其消費支出是16.9億元。
由於線性插值法只利用兩點的對應值宋推算兩點之間的對應值,而兩點對應值本身往往受到各種偶然因素的影響,所以線性插值結果可能誤差較大。
評論(共14條)
這個是我二十年前研究出的公式,發表在《管理會計》,正名叫:“以直代曲解析公式法”,還有一組叫“以曲代曲解析公式法”。現在的一些教科書引用了,改名為:線性插入、一般公式、特殊公式……都是篡改。智庫的插圖解析就是一大笑話:直線圖形不該是右高左低,應該是左高右低,因為折現率與凈現值是呈反比例關係的。 劉雲
這個是我二十年前研究出的公式,發表在《管理會計》,正名叫:“以直代曲解析公式法”,還有一組叫“以曲代曲解析公式法”。現在的一些教科書引用了,改名為:線性插入、一般公式、特殊公式……都是篡改。智庫的插圖解析就是一大笑話:直線圖形不該是右高左低,應該是左高右低,因為折現率與凈現值是呈反比例關係的。 劉雲
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯!








缺少實際例題解說