納什嵌入定理
出自 MBA智库百科(https://wiki.mbalib.com/)
納什嵌入定理((Nash Embedding Theorem)
目錄 |
納什嵌入定理是指以約翰·福布斯·納什命名，指出每個黎曼流形可以等距嵌入到歐幾裡得空間Rn。
“等距”表示“保持曲線長度”。因此，該結果表明每個黎曼流形可以看作是歐幾裡得空間的子流形。第一個定理適用於C1-光滑嵌入，第二個用於解析或Ck, 3 ≤k≤∞的情形。兩個定理非常不同；第一個有很簡單的證明但並不直觀，而第二個非常具有技術性但其結論並不讓人吃驚。
C1定理髮表於1954年，Ck定理髮表於1956年，解析的情形則發表於1966年，都由納什給出。其深入發展見h-原則。
定理:令(M,g)為一黎曼流形而f:Mm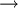
Rn為一個短的
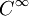光滑嵌入（或浸入(immersion)）到歐幾裡得空間Rn, n
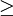m+1。則對於任意ε>0存在嵌入(或浸入)fε:Mm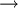Rn滿足
(i)C1-光滑,
(ii)等距，也即對於在點x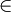
M的切空間任何兩個向量v,w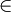Tx(M)，我們有g(v,w)=
,
。
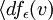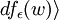(iii)ε-接近f,i.e.:|f(x)-fε(x)|<ε對於所有x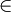M。
特別的是，因為它從惠特尼嵌入定理（Whitney embedding theorem）得出，任何m-維黎曼流形可以有一個等距C1-嵌入到2m-維歐幾裡得空間。定理最初由納什在條件n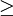m+2 而不是n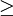m+1下證明，爾後被尼古拉·科伊伯(Nicolaas Kuiper)推廣，用的是一個相對簡單的技巧。
定理有很多反直觀的暗示。例如，可以得出任何閉可定向曲面可以C1嵌入到在歐幾裡得三維空間中的任意小球(根據高斯公式,不存在這樣的C2-嵌入)。
Ck嵌入定理:
技術性的陳述如下: 若M為一給定m-維黎曼流形 (解析或屬於Ck類, 3 ≤k≤∞), 則存在n(n=m2+5m+3 就可以)和一個單射f: M ->Rn (也是解析的或者屬於Ck類)使得對於M的所有點p，導數dfp是一個線性映射從切空間TpM到\Rn，和給定在TpM上的內積和\Rn的標準內積在如下意義下兼容:
< u , v> = dfp(u) • dfp(v)
對於TpM中的所有向量u,v。這是偏微分方程(PDE)的不定系統。
納什嵌入定理是全局系統，因為整個流形嵌入到了\Rn。局部嵌入定理要簡單得多，可以通過隱函數定理證明。這裡給出的全局嵌入定理的證明依賴於納什對隱函數定理的極大推廣版本，Nash-Moser定理和帶後處理(postconditioning)的牛頓法。納什解決嵌入問題的基本思想是採用牛頓法來證明該PDE系統有解。標準的牛頓法應用於該系統時不收斂，所以納什利用光滑化運算元來保證牛頓迴圈收斂。這個改變了的牛頓法成為帶後處理的牛頓法。平滑運算元由捲積定義。該平滑運算元保證了迴圈的趨向於一個根，使得它可以用來作為存在性定理。通過證明PDE系統存在一個根就證明瞭黎曼流形的等距嵌入的存在性。有一個更老的迴圈稱為Kantovorich迴圈，它是只用牛頓方法的存在性定理(所以不用平滑運算元)。
