均勻設計
出自 MBA智库百科(https://wiki.mbalib.com/)
均勻設計(Uniform Design)
目錄 |
均勻設計(Uniform Design)是一種試驗設計方法(Experimental Design Method),稱為均勻設計(Uniform Design)或均勻設計試驗法(Uniform Design Experimentation),或空間填充設計。
所有的試驗設計方法本質上都是在試驗的範圍內給出挑選代表性點的方法,均勻設計也不例外,它是只考慮試驗點在試驗範圍內均勻散佈的一種試驗設計方法。它由方開泰教授和數學家王元在1978年共同提出,是數論方法中的“偽蒙特卡羅方法”的一個應用。
均勻設計是繼60年代華羅庚教授倡導、普及的優選法和我國數理統計學者在國內普及推廣的正交法之後,於70年代末應航天部第三研究院飛航導彈火控系統建立數學模型、並研究其諸多影響因素的需要,由中國科學院應用數學所方開泰教授和王元教授提出的一種試驗設計方法。均勻設計是統計試驗設計的方法之一,它與其它的許多試驗設計方法,如正交設計、最優設計、旋轉設計、穩健設計和貝葉斯設計等相輔相成。
我們知道,試驗設計就是如何在試驗域內最有效地選擇試驗點,通過試驗得到響應的觀測值,然後進行數據分析求得達到最優響應值的試驗條件。因此,試驗設計的目標,就是要用最少的試驗取得關於系統的儘可能充分的信息。均勻設計即可以較好地實現這一目標,尤其對多因素、多水平的試驗。
均勻設計的數學原理是數論中的一致分佈理論,此方法借鑒了“近似分析中的數論方法”這一領域的研究成果,將數論和多元統計相結合,是屬於偽蒙特卡羅方法的範疇。均勻設計只考慮試驗點在試驗範圍內均勻散佈,挑選試驗代表點的出發點是“均勻分散”,而不考慮“整齊可比”,它可保證試驗點具有均勻分佈的統計特性,可使每個因素的每個水平做一次且僅做一次試驗,任兩個因素的試驗點點在平面的格子點上,每行每列有且僅有一個試驗點。它著重在試驗範圍內考慮試驗點均勻散佈以求通過最少的試驗來獲得最多的信息,因而其試驗次數比正交設計明顯的減少,使均勻設計特別適合於多因素多水平的試驗和系統模型完全未知的情況。例如,當試驗中有m個因素,每個因素有n個水平時,如果進行全面試驗,共有nm種組合,正交設計是從這些組合中挑選出n2個試驗,而均勻設計是利用數論中的一致分佈理論選取n個點試驗,而且應用數論方法使試驗點在積分範圍內散佈得十分均勻,並使分佈點離被積函數的各種值充分接近,因此便於電腦統計建模。如某項試驗影響因素有5個,水平數為1O個,則全面試驗次數為105次,即做十萬次試驗;正交設計是做102次,即做100次試驗;而均勻設計只做10次,可見其優越性非常突出。
均勻設計是通過一套精心設計的表來進行試驗設計的,對於每一個均勻設計表都有一個使用表,可指導如何從均勻設計表中選用適當的列來安排試驗。均勻設計分會還編製了一套軟體《均勻設計與統計調優軟體包》供試驗設計和數據處理、分析使用,非常方便。均勻設計法的試驗數據分析要用到回歸分析方法,例如線性回歸模型、二次回歸模型、非線性回歸模型,以及各種選擇回歸變點的方法,也有利用多元樣條函數技術、小波理論、人工神經網路模型應用於試驗設計和數據分析。具體選擇何種模型要根據實際試驗的具體性質來確定。利用回歸分析得出的模型,即可進行影響因素的重要性分析及新條件試驗的結果估算,預報和最優化。
近幾年來,均勻設計理論研究突飛猛進,對均勻設計和其它試驗設計的關聯和結合,如與正交設計進行了均勻性、最優性比較研究,得出在大多數情況下,特別是模型比較複雜時,均勻設計試驗次數少、均勻性好,並對非線性模型有較好的估計。對線性模型,均勻設計有較好的均勻性和較少的試驗次數,正交設計有較好的估計。雖然均勻設計失去了正交設計的整齊可比性,但在選點方面比正交設計有更大的靈活性,也就是說,它更加註重了均勻性.利用均勻設計可以選到偏差更小的點,更重要的是,試驗次數由108減少到n,從而在實踐中大大降低了成本。從經濟和優化兩個角度衡量,均勻設計確實有其優越性。實踐中若水平數多,因素多而要求試驗次數少的設計,一般用均勻設計來安排試驗;對於因素數,水平數不多,一般採用正交設計。有時,可以將正交設計和均勻設計結合起來使用。
有論文對均勻設計經濟效益評估數理模型進行了探討,並與全面試驗、正交設計作了比較。也有論文對均勻設計的優良性進行了研究,指出還有待進一步發掘,對均勻性本身也還有很多數學背景值得進一步研究。也有論文認為利用模糊理論與均勻設計結合,建立模糊集台數據群,再通過因素與水平選擇,建立模糊模擬均勻設計表,進行數據統計分析、調優,反向推斷。這種模糊理論—— 均勻設計——統計調優的有機結合對某些項目的反設計會有廣闊的應用前景。對應用中的一些問題,如因素與水平的選擇 模型的建立提出了很好的建議,指出一個試驗成功的關鍵在於選擇合適的因素和有關的試驗範圍,如果重要的因素沒有選人試驗,則試驗效果將大受影響,甚至失敗,因而在不增加試驗數目的前提下,儘可能多選出一些因素,通過試驗來篩選}並採用多水平試驗以獲得因素和響應之間較為豐富的關係,否則因素主效應和交互效應將會混雜,不能估出,直接影響試驗的效果。對模型未知(包括部分模型已知)時,應進行適當的重覆試驗有助於模型識別,尤其當隨機誤差很大時,沒有適當的重覆試驗,很難得到可靠的結論.從應用的角度,對理論研究也提出了新的需求,希望能設計出水平數更多的均勻設計表。
1.試驗次數大大減少。例如某化工試驗,欲找出最優產量或其它優化目標條件。試驗因素3個,每因素在取值範圍內均有7個試驗點。
- 採用優選法:對多因素同時選優的試驗,不適用。
- 採用正交法:需做49次試驗,方可找出最優產量或其它優化目標條件。
- 採用均勻設計:只需做7次試驗即可。
2.自動將各試驗因素分類為重要與次要,並將因素按重要性排序。
3.過程數字化,通過電腦對結果與因素條件進行界定與預報(如天氣預報),進而控制各因素。
1、明確試驗目的, 確定試驗指標。若考察的指標有多個則一般需要對指標進行綜合分析;
2、選擇試驗因素。根據專業知識和實際經驗進行試驗因素的選擇, 一般選擇對試驗指標影響較大的因素進行試驗;
3、確定因素水平。根據試驗條件和以往的實踐經驗, 首先確定各因素的取值範圍, 然後在此範圍內設置適當的水平;
4、選擇均勻設計表, 排布因素水平。根據因素數、水平數來選擇合適的均勻設計表進行因素水平數據排布;
5、明確試驗方案, 進行試驗操作;
6、試驗結果分析。建議採用回歸分析方法對試驗結果進行分析進而發現優化的試驗條件。依試驗目的和支持條件的不同也可採用直接觀察法取得最好的試驗條件(不再進行數據的分析處理);
7、優化條件的試驗驗證。通過回歸分析方法計算得出的優化試驗條件一般需要進行優化試驗條件的實際試驗驗證(可進一步修正回歸模型);
8、縮小試驗範圍進行更精確的試驗, 尋找更好的試驗條件, 直至達到試驗目的為止。
1、當所研究的因素和水平數目較多時, 均勻設計試驗法比其它試驗設計方法所需的試驗次數更少, 但不可過分追求少的試驗次數, 除非有很好的前期工作基礎和豐富的經驗, 否則不要企圖通過做很少的試驗就可達到試驗目的, 因為試驗結果的處理一般需要採用回歸分析方法完成, 過少的試驗次數很可能導致無法建立有效的模型, 也就不能對問題進行深入的分析和研究, 最終使試驗和研究停留在錶面化的水平上(無法建立有效的模型, 只能採用直接觀察法選擇最佳結果)。一般情況下, 建議試驗的次數取因素數的3~5倍為好;
2、優先選用 表進行試驗設計。通常情況下
表進行試驗設計。通常情況下 表的均勻性要好於Un表, 其試驗點布點均勻, 代表性強, 更容易揭示出試驗的規律, 而且在各因素水平序號和實際水平值順序一致的情況還可避免因各因素最大水平值相遇所帶來的試驗過於劇烈或過於緩慢而無法控制的問題;
表的均勻性要好於Un表, 其試驗點布點均勻, 代表性強, 更容易揭示出試驗的規律, 而且在各因素水平序號和實際水平值順序一致的情況還可避免因各因素最大水平值相遇所帶來的試驗過於劇烈或過於緩慢而無法控制的問題;
3、對於所確定的優化試驗條件的評價, 一方面要看此條件下指標結果的好壞, 另一方面要考慮試驗條件是否合理可行的問題, 要權衡利弊, 力求達到用最小的付出獲取最大收益的效果。
回顧幾十多年來均勻設計法的誕生、發展和廣泛應用,有如下幾個鮮明的特點:
(1)均勻設計法的誕生是應國防科研實踐的需求,由我國科學家潛心研究、開發的,其來自於實踐,又應用於實踐,實踐促進研究,研究又進一步指導實踐,理論研究與實踐應用相輔相成,互為依存、互相促進,創造更大效益;
(2)均勻設計法的創立和實際應用的意義,錢學森、朱光亞等老一輩科學家以其敏銳的科學目光和判斷,給予了高度評價,同時也得到了原國防科工委領導的重視和支持.專家和領導的支持、重視是一項新技術快速發展的必不可少的重要條件;
(3)1994年成立了中國數學會均勻設計分會,原國防科工委將均勻設計法的推廣應用納入“八五”國防科技成果重點項目推廣計劃,有力地推動了均勻設計法的發展;
(4)均勻設計法的理論研究和推廣應用也得益於各部門領導的支持以及專家與廣大科技工作者科學求實、積極不懈地努力;
(5)學會與各地區、各部門相結合,開發均勻設計軟體、攝製推廣錄像片、進行技術培訓和學術交流,推動了均勻設計法的理論研究和應用實踐。
均勻設計正是由於上述的理論與實踐結合、領導與群眾結台、專家與廣大科技工作者結合、行政組織與學會結台,不斷發展、完善,不斷拓展新的應用領域,為增強我國的經濟實力和國防科技的發展做出了很大貢獻。今後,應進一步發揮學會組織和各地區、各部門的力量,調動各方面的積極性,充分利用互聯網的優勢,相互支持、密切協同,有組織、有計劃地使均勻設計的理論研究與實踐應用取得更大的發展,為國民經濟和國防現代化做出更大的貢獻。
均勻設計與正交設計的比較[1]
在均勻設計方法出現以前,正交設計已經在工農業生產中廣泛應用,並取得良好效果。基於推廣均勻設計方法的考慮,作為一種新的試驗設計方法,人們自然而然地會拿正交設計與均勻設計相比較。通過與正交設計進行均勻性、最優性的比較發現:
(1)在試驗數相同情況下均勻設計的均勻性比正交設計好得多,在大多數情況下,特別是模型比較複雜時,均勻設計方法的試驗次數少、均勻性好,並對非線性模型有較好的估計。對線性模型均勻設計有較好的均勻性和較少的試驗次數。
(2)水平數相同或偏差相近時,均勻設計的試驗次數相對於正交設計有絕對優勢。雖然均勻設計失去了正交設計的整齊可比性,但在選點方面比正交設計具有更大的靈活性,也就是說,它更加註重了均勻性,利用均勻設計的均勻分散性可以選到偏差更小的點;更重要的是,試驗次數由n2減少到n。因此均勻設計的試驗次數隨水平增加有連續性,而正交設計有“跳躍性”,從而在實踐中大大降低了成本,適合於多因素多水平試驗。
(3)正交設計的數據分析程式簡單,且直觀分析可以給出試驗指標隨每個水平變化的規律;均勻設計的數據可用回歸分析、最優化和關聯度分析等方法來處理一般要用電腦。有時也可以根據優化原則從試驗點中挑選一個最優指標,雖然粗糙但卻非常有效適合於缺少計算工具的情況。
均勻設計的這些特點使它適合於岩土工程領域。首先,岩土工程中存在大量的非線性關係;其次對模型未知的工程問題,可以利用均勻設計方法進行優化設計。
均勻設計的案例分析[1]
近年來,隨著均勻設計理論的日趨成熟,均勻設計方法逐漸被岩土工程領域的研究人員採用,如進行電腦試驗設計、反分析、配料設計、參數優化等研究。以下通過三峽永久船閘高邊坡岩體力學參數三維位移反分析來說明均勻設計方法在岩土工程領域的應用。
1.計算條件
計算區域包括三峽永久船閘二、三閘室,區域內有全強風化、弱風化、微新岩體及F215,f5斷層。主要反演卸荷變形區和損傷鬆動區的粘聚力c、摩擦繫數f與彈性模量E,其他區域介質的c,f,E與地應力場不參與反演。反演的初始數據為進入閘室開挖以後的幾個階段開挖引起的位移增量。通過模擬邊坡施工過程,分11步開挖進行反演分析。
2.樣本構造
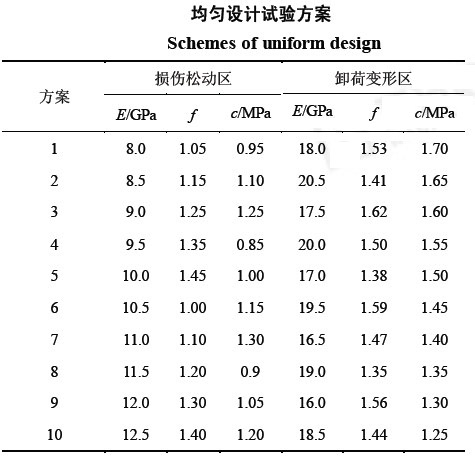
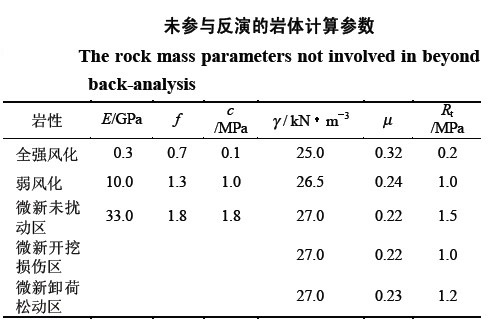
根據歷年來在三峽船閘區的試驗資料和二維反演分析結果將微新岩體損傷鬆動區和卸荷變形區的彈性模量E及其強度參數(f,c)考慮為均勻試驗設計的6個因素,取值範圍見表1。在樣本試驗階段,將每個參數區間等分為10個水平,查均勻設計表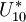 (108)得正分析的參數組合方案(下表)。第二個表中列出了不參與反演的岩體物理力學參數。
(108)得正分析的參數組合方案(下表)。第二個表中列出了不參與反演的岩體物理力學參數。
3.反分析目標函數
用優化方法進行位移反分析的實質就是尋找一組待反演的參數使與其相應的位移值與實測位移值逼近的方法。對於實際工程的設計和施工來說,這種逼近追求的是總體上的最優效果,因此,目標函數通常取為以下形式:
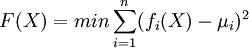 (1)
(1)
或類似的形式
式中: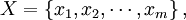 xm為待反演的岩體參數,如彈性摸量E、粘聚力c、摩擦繫數f等;m為待反演的岩體參數個數;fi(X)為岩體在第i個量測點上發生的位移量的計算值,ui為相應的位移量的實測值;n為位移量測點的總數。
xm為待反演的岩體參數,如彈性摸量E、粘聚力c、摩擦繫數f等;m為待反演的岩體參數個數;fi(X)為岩體在第i個量測點上發生的位移量的計算值,ui為相應的位移量的實測值;n為位移量測點的總數。
4.反演分析結果
為了反演分析的需要均取進入閘室開挖以後至閘底的觀測時段的位移增量。用於反演的測點有剖面13-13的TP/BM46GP01,TP/BM47GP01、TP/BM49GP01,TP/BM67GP01;剖面17-17的TP/BM27GP02,TP/BM28GP02,TP/BM29GP02,TP/BM98GP02,TP/BM10GP01,TP/BM11GP01,TP/BM71GP01;和剖面20-20的TP/BM13GP01,TP/BM14GP01,TP/BM72GP01,TP/BM34GP02,TP/BM36GP02,TP/BM99GP02共17個測點。
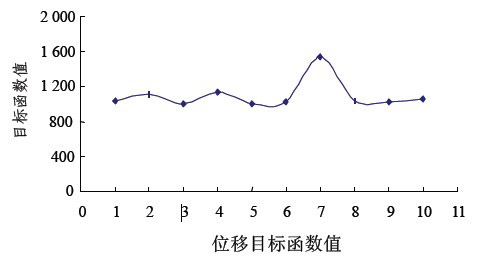
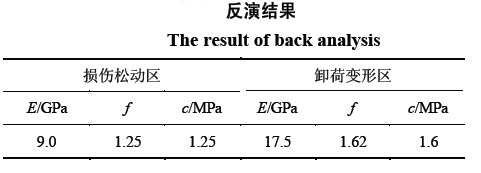
對於均勻設計試驗方案表中每一組試驗組合,作正分析計算將以上17個測點處的x方向(垂直於船閘軸線的水平方向)位移計算值和實測值代入式(1)得10個計算方案的目標函數值如下圖;由此分析得到的岩體參數見下表。
5.反演參數正分析
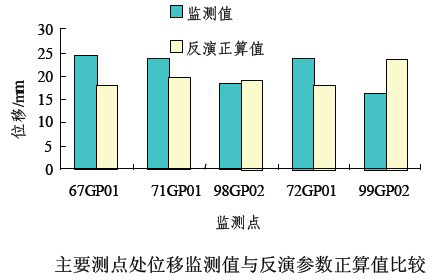
用反演得出的參數正向計算出的位移和主要測點實測位移值的比較見下圖,從下圖看,結果是較令人滿意的。








有用,頂