瓦爾拉斯的一般均衡模型
出自 MBA智库百科(https://wiki.mbalib.com/)
瓦爾拉斯的一般均衡模型(Walrasian General Equilibrium Model)
目錄 |
早在1874年,法國經濟學家里昂·瓦爾拉斯就建立了一套被後人稱為瓦爾拉斯一般均衡的理論(Walrasian General Equilibrium Theory)。在經濟學說史上,瓦爾拉斯第一個提出了一般均衡的數學模型並試圖解決一般均衡的存在性問題。
瓦爾拉斯按照從簡單到複雜的思路一步一步地構建自己的一般均衡理論體系。首先,他從產品市場著手來考察交換的一般均衡,而後從要素市場的角度來考察包括生產過程的一般均衡,然後再對資本積累進行一般均衡分析,最後他還運用一般均衡分析方法考察了貨幣交換和貨幣窖藏的作用而得出了他的“貨幣和流通理論”,從而把一般均衡理論由實物經濟推廣到貨幣經濟。瓦爾拉斯的一般均衡理論後經帕累托、希克斯、諾伊曼、薩繆爾森、阿羅、德布魯以及麥肯齊等經濟學家的改進和發展之後,形成為現代一般均衡理論。
瓦爾拉斯認為,當滿足商品的效用或欲望方程式和最初所擁有的商品數量這兩個條件時,均衡價格就可以確定了。也就是說,在純交換經濟中,進入市場的參與者帶著既定數量的商品作為供給,根據他們的效用或欲望即需求進行交換,必定能達到均衡。用Si表示進入市場進行交換的第種i商品的供給量(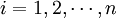 );用Pi表示第i種商品的價格(
);用Pi表示第i種商品的價格(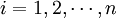 );用Di表示第i種商品的需求量(
);用Di表示第i種商品的需求量(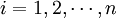 )。如果第i種商品的需求量不僅受到其本身價格的影響,而且還受到其他商品價格的影響,那麼需求函數可表示為:
)。如果第i種商品的需求量不僅受到其本身價格的影響,而且還受到其他商品價格的影響,那麼需求函數可表示為:
 (1.1)
(1.1)
按照上述定義,當存在一組價格Pe時,瓦爾拉斯一般均衡模型可表述為:
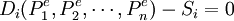
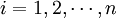 (1.2)
(1.2)
但(1.2)式所表示的幾種商品的需求方程並不是完全獨立的,只有(改:而是)通過供求均衡約束條件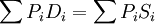 而相互關聯。這個恆等式表明,就整個交換來說,在任何一組價格下,需求總量必須與供給總量相等。即在整個交換中,供給和需求雙方相互受到對方的約束。
而相互關聯。這個恆等式表明,就整個交換來說,在任何一組價格下,需求總量必須與供給總量相等。即在整個交換中,供給和需求雙方相互受到對方的約束。
在恆等式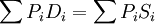 的約束下,方程組
的約束下,方程組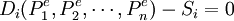 只有n − 1個獨立方程,而待解的商品價格有n個。為了能夠求解,瓦爾拉斯引入法定價值作為商品價格的計算單位。令某一商品的價格如商品1的價格為法定價值,則其他商品價格可以用P1來計算,記為
只有n − 1個獨立方程,而待解的商品價格有n個。為了能夠求解,瓦爾拉斯引入法定價值作為商品價格的計算單位。令某一商品的價格如商品1的價格為法定價值,則其他商品價格可以用P1來計算,記為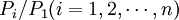 。這樣商品1的價格等於1,其他商品價格表現為和商品1的價格相比的相對價格。需求函數變成:
。這樣商品1的價格等於1,其他商品價格表現為和商品1的價格相比的相對價格。需求函數變成:
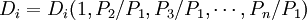 (1.3)
(1.3)
這樣價格變數就變為n1個相對價格。運用n1個獨立的方程式,求解個相對價格,均衡價格可以得到。
由於引入法定價值,得到的均衡價格是相對價格,即解得的均衡價格都要乘上某一個常數。恆等式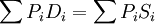 被稱為瓦爾拉斯定律,即種商品的需求和供給中,如果當n1種商品處於均衡狀態,則餘下的一種也必然處於均衡狀態。同時也說明如果存在某種商品的超額需求,必然就存在某些商品的超額供給與之對應,且數量相等。這也就是說,在整個經濟系統內部,存在著供求均衡的自動調節機制,通過價格的伸縮,可以調節超額供給與超額需求,最後使之達到均衡。
被稱為瓦爾拉斯定律,即種商品的需求和供給中,如果當n1種商品處於均衡狀態,則餘下的一種也必然處於均衡狀態。同時也說明如果存在某種商品的超額需求,必然就存在某些商品的超額供給與之對應,且數量相等。這也就是說,在整個經濟系統內部,存在著供求均衡的自動調節機制,通過價格的伸縮,可以調節超額供給與超額需求,最後使之達到均衡。
由於市場由消費者和生產者兩類行為主體構成,則可以將市場分為生產要素和商品兩個市場。這樣,瓦爾拉斯一般均衡模型可以由以下5個方程組來進行表述:
⑴ 生產要素的需求方程
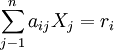 (1.4)
(1.4)
當生產技術既定不變,規模報酬也不改變以及各種要素都被充分利用的條件下,方程式(1.4)式左邊所表示的對生產要素的需求量等於該式右邊所表示的生產需求量,也就是生產要素市場處於均衡狀態。其中,(1.4)式中的aij表示生產技術繫數,Xj為第j種商品的生產量,ri表示生產中所使用的第i種生產要素。
⑵ 商品的需求方程

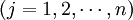 (1.5)
(1.5)
公式(1.5)中的Pj為第j種商品的價格,Vj為第j種生產要素的價格。引入要素價格即生產要素所有者的收入,說明人們對某種商品的需求量不僅取決於各種商品的價格,而且還取決於人們的收入。事實上,它與前述的需求函數是一致的,這裡只不過是把價格區分為商品價格和生產要素價格。
⑶ 成本方程或商品供給方程
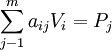
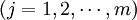 (1.6)
(1.6)
公式(1.6)左邊表示單位商品的生產成本,由於假定商品市場是完全競爭市場,因而長期均衡的商品價格等於各種商品每一單位的成本,而該式右邊Pj的種商品就是第j種商品的均衡價格。所以該方程又表示了價格的形成,故又稱為價格方程。
⑷ 生產要素的供給方程
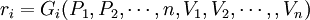
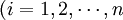 (1.7)
(1.7)
公式(1.7)說明,生產要素的供給,不僅決定於該要素的價格,而且還決定於其他要素和其他商品的價格。
⑸ 均衡條件
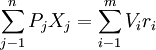 (1.8)
(1.8)
像交換的一般均衡一樣,從式(1.4)到式(1.7)4個方程中所表示的種商品和種生產要素的供求方程並不是完全獨立的,也需要通過供求均衡約束而相互關聯。
由於均衡條件可以從公式(1.4)和公式(1.6)中推導出來,模型中獨立的方程個數為2m+2n-1個,變數個數為2m+2n個,因此仍需要引入法定價格,使變數個數減少為2m+2n-1個,才能使模型有解。解出的價格向量同樣是相對價格向量。
瓦爾拉斯均衡模型體現了一般均衡分析的基本思想,但遺憾的是,它對一般均衡價格的存在性的說明缺乏說服力,因為即使體系中未知價格變數的個數和方程的個數相等,但也並不能保證得到一個解。事實上,未知價格變數的個數等於方程個數的條件,既不是一組方程有解的必要條件,也不是充分條件。即使是一個方程組有解,但又有什麼理由斷定這些解一定是正數值呢?對此,瓦爾拉斯不得不推演出一種方式,通過一系列連續的近似來逼近均衡解。這種方式,瓦爾拉斯稱之為退約調整過程,並用這種程式來模擬市場實際發生的交換過程。根據這一方法,市場機構通過反覆試驗來“感覺”和“摸索”逼近均衡的途徑。假定市場過程中存在一個拍賣者來組織交易的進行。商品的交換中,由拍賣者喊價,由交易都隨著喊出的價格調整供求,直到供求相等而成交,首次喊價是隨意的,隨後就在喊價的基礎上,比較供給與需求的意願。如果它們不一致,則第二次喊價根據供求意願的相對情況,對有超額需求意願的商品提高價格,對有超額供給意願的商品降低價格,從而逐步接近均衡。這就是瓦爾拉斯一般均衡的“試探過程”。
當然,在現實的經濟中根本不存在瓦爾拉斯所設想的拍賣者。針對瓦爾拉斯一般均衡所存在的上述問題,經濟學家們包括帕累托、希克斯、諾伊曼、薩繆爾森、阿羅、德布魯和麥肯齊等人對一般均衡理論給予了改進和發展。尤其是20世紀五六十年代,阿羅和德布魯對一般均衡存在性的公理化證明,更是奠定了現代西方經濟學中一般均衡理論的基礎。
- 湖南大學.《西方經濟學》.第十章 一般均衡理論和福利經濟學.第一節,一般均衡理論.二、瓦爾拉斯的一般均衡模型







