瓦尔拉斯的一般均衡模型
出自 MBA智库百科(https://wiki.mbalib.com/)
瓦尔拉斯的一般均衡模型(Walrasian General Equilibrium Model)
目录 |
早在1874年,法国经济学家里昂·瓦尔拉斯就建立了一套被后人称为瓦尔拉斯一般均衡的理论(Walrasian General Equilibrium Theory)。在经济学说史上,瓦尔拉斯第一个提出了一般均衡的数学模型并试图解决一般均衡的存在性问题。
瓦尔拉斯按照从简单到复杂的思路一步一步地构建自己的一般均衡理论体系。首先,他从产品市场着手来考察交换的一般均衡,而后从要素市场的角度来考察包括生产过程的一般均衡,然后再对资本积累进行一般均衡分析,最后他还运用一般均衡分析方法考察了货币交换和货币窖藏的作用而得出了他的“货币和流通理论”,从而把一般均衡理论由实物经济推广到货币经济。瓦尔拉斯的一般均衡理论后经帕累托、希克斯、诺伊曼、萨缪尔森、阿罗、德布鲁以及麦肯齐等经济学家的改进和发展之后,形成为现代一般均衡理论。
瓦尔拉斯认为,当满足商品的效用或欲望方程式和最初所拥有的商品数量这两个条件时,均衡价格就可以确定了。也就是说,在纯交换经济中,进入市场的参与者带着既定数量的商品作为供给,根据他们的效用或欲望即需求进行交换,必定能达到均衡。用Si表示进入市场进行交换的第种i商品的供给量(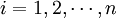 );用Pi表示第i种商品的价格(
);用Pi表示第i种商品的价格(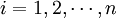 );用Di表示第i种商品的需求量(
);用Di表示第i种商品的需求量(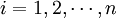 )。如果第i种商品的需求量不仅受到其本身价格的影响,而且还受到其他商品价格的影响,那么需求函数可表示为:
)。如果第i种商品的需求量不仅受到其本身价格的影响,而且还受到其他商品价格的影响,那么需求函数可表示为:
 (1.1)
(1.1)
按照上述定义,当存在一组价格Pe时,瓦尔拉斯一般均衡模型可表述为:
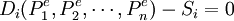
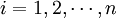 (1.2)
(1.2)
但(1.2)式所表示的几种商品的需求方程并不是完全独立的,只有(改:而是)通过供求均衡约束条件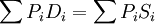 而相互关联。这个恒等式表明,就整个交换来说,在任何一组价格下,需求总量必须与供给总量相等。即在整个交换中,供给和需求双方相互受到对方的约束。
而相互关联。这个恒等式表明,就整个交换来说,在任何一组价格下,需求总量必须与供给总量相等。即在整个交换中,供给和需求双方相互受到对方的约束。
在恒等式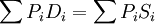 的约束下,方程组
的约束下,方程组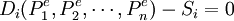 只有n − 1个独立方程,而待解的商品价格有n个。为了能够求解,瓦尔拉斯引入法定价值作为商品价格的计算单位。令某一商品的价格如商品1的价格为法定价值,则其他商品价格可以用P1来计算,记为
只有n − 1个独立方程,而待解的商品价格有n个。为了能够求解,瓦尔拉斯引入法定价值作为商品价格的计算单位。令某一商品的价格如商品1的价格为法定价值,则其他商品价格可以用P1来计算,记为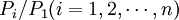 。这样商品1的价格等于1,其他商品价格表现为和商品1的价格相比的相对价格。需求函数变成:
。这样商品1的价格等于1,其他商品价格表现为和商品1的价格相比的相对价格。需求函数变成:
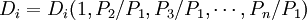 (1.3)
(1.3)
这样价格变量就变为n1个相对价格。运用n1个独立的方程式,求解个相对价格,均衡价格可以得到。
由于引入法定价值,得到的均衡价格是相对价格,即解得的均衡价格都要乘上某一个常数。恒等式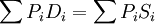 被称为瓦尔拉斯定律,即种商品的需求和供给中,如果当n1种商品处于均衡状态,则余下的一种也必然处于均衡状态。同时也说明如果存在某种商品的超额需求,必然就存在某些商品的超额供给与之对应,且数量相等。这也就是说,在整个经济系统内部,存在着供求均衡的自动调节机制,通过价格的伸缩,可以调节超额供给与超额需求,最后使之达到均衡。
被称为瓦尔拉斯定律,即种商品的需求和供给中,如果当n1种商品处于均衡状态,则余下的一种也必然处于均衡状态。同时也说明如果存在某种商品的超额需求,必然就存在某些商品的超额供给与之对应,且数量相等。这也就是说,在整个经济系统内部,存在着供求均衡的自动调节机制,通过价格的伸缩,可以调节超额供给与超额需求,最后使之达到均衡。
由于市场由消费者和生产者两类行为主体构成,则可以将市场分为生产要素和商品两个市场。这样,瓦尔拉斯一般均衡模型可以由以下5个方程组来进行表述:
⑴ 生产要素的需求方程
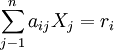 (1.4)
(1.4)
当生产技术既定不变,规模报酬也不改变以及各种要素都被充分利用的条件下,方程式(1.4)式左边所表示的对生产要素的需求量等于该式右边所表示的生产需求量,也就是生产要素市场处于均衡状态。其中,(1.4)式中的aij表示生产技术系数,Xj为第j种商品的生产量,ri表示生产中所使用的第i种生产要素。
⑵ 商品的需求方程

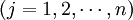 (1.5)
(1.5)
公式(1.5)中的Pj为第j种商品的价格,Vj为第j种生产要素的价格。引入要素价格即生产要素所有者的收入,说明人们对某种商品的需求量不仅取决于各种商品的价格,而且还取决于人们的收入。事实上,它与前述的需求函数是一致的,这里只不过是把价格区分为商品价格和生产要素价格。
⑶ 成本方程或商品供给方程
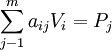
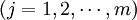 (1.6)
(1.6)
公式(1.6)左边表示单位商品的生产成本,由于假定商品市场是完全竞争市场,因而长期均衡的商品价格等于各种商品每一单位的成本,而该式右边Pj的种商品就是第j种商品的均衡价格。所以该方程又表示了价格的形成,故又称为价格方程。
⑷ 生产要素的供给方程
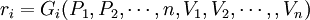
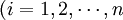 (1.7)
(1.7)
公式(1.7)说明,生产要素的供给,不仅决定于该要素的价格,而且还决定于其他要素和其他商品的价格。
⑸ 均衡条件
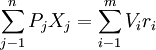 (1.8)
(1.8)
像交换的一般均衡一样,从式(1.4)到式(1.7)4个方程中所表示的种商品和种生产要素的供求方程并不是完全独立的,也需要通过供求均衡约束而相互关联。
由于均衡条件可以从公式(1.4)和公式(1.6)中推导出来,模型中独立的方程个数为2m+2n-1个,变量个数为2m+2n个,因此仍需要引入法定价格,使变量个数减少为2m+2n-1个,才能使模型有解。解出的价格向量同样是相对价格向量。
瓦尔拉斯均衡模型体现了一般均衡分析的基本思想,但遗憾的是,它对一般均衡价格的存在性的说明缺乏说服力,因为即使体系中未知价格变量的个数和方程的个数相等,但也并不能保证得到一个解。事实上,未知价格变量的个数等于方程个数的条件,既不是一组方程有解的必要条件,也不是充分条件。即使是一个方程组有解,但又有什么理由断定这些解一定是正数值呢?对此,瓦尔拉斯不得不推演出一种方式,通过一系列连续的近似来逼近均衡解。这种方式,瓦尔拉斯称之为退约调整过程,并用这种程序来模拟市场实际发生的交换过程。根据这一方法,市场机构通过反复试验来“感觉”和“摸索”逼近均衡的途径。假定市场过程中存在一个拍卖者来组织交易的进行。商品的交换中,由拍卖者喊价,由交易都随着喊出的价格调整供求,直到供求相等而成交,首次喊价是随意的,随后就在喊价的基础上,比较供给与需求的意愿。如果它们不一致,则第二次喊价根据供求意愿的相对情况,对有超额需求意愿的商品提高价格,对有超额供给意愿的商品降低价格,从而逐步接近均衡。这就是瓦尔拉斯一般均衡的“试探过程”。
当然,在现实的经济中根本不存在瓦尔拉斯所设想的拍卖者。针对瓦尔拉斯一般均衡所存在的上述问题,经济学家们包括帕累托、希克斯、诺伊曼、萨缪尔森、阿罗、德布鲁和麦肯齐等人对一般均衡理论给予了改进和发展。尤其是20世纪五六十年代,阿罗和德布鲁对一般均衡存在性的公理化证明,更是奠定了现代西方经济学中一般均衡理论的基础。
- 湖南大学.《西方经济学》.第十章 一般均衡理论和福利经济学.第一节,一般均衡理论.二、瓦尔拉斯的一般均衡模型







