TOPSIS法
出自 MBA智库百科(https://wiki.mbalib.com/)
TOPSIS法(Technique for Order Preferenceby Similarity to Ideal Solution,)逼近理想解排序法、理想點法
目錄 |
TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution )法是C.L.Hwang和K.Yoon於1981年首次提出,TOPSIS法根據有限個評價對象與理想化目標的接近程度進行排序的方法,是在現有的對象中進行相對優劣的評價。理想化目標(Ideal Solution)有兩個,一個是肯定的理想目標(positive ideal solution)或稱最優目標,一個是否定的理想目標(negative ideal solution)或稱最劣目標,評價最好的對象應該是與最優目標的距離最近,而與最劣目標最遠,距離的計算可採用明考斯基距離,常用的歐幾里德幾何距離是明考斯基距離的特殊情況。
TOPSIS法是一種理想目標相似性的順序選優技術,在多目標決策分析中是一種非常有效的方法。它通過歸一化後的數據規範化矩陣,找出多個目標中最優目標和最劣目標(分別用理想解和反理想解表示) ,分別計算各評價目標與理想解和反理想解的距離,獲得各目標與理想解的貼近度,按理想解貼近度的大小排序,以此作為評價目標優劣的依據。貼近度取值在0~1 之間,該值愈接近1,表示相應的評價目標越接近最優水平;反之,該值愈接近0,表示評價目標越接近最劣水平。該方法已經在土地利用規劃、物料選擇評估、項目投資、醫療衛生等眾多領域得到成功的應用,明顯提高了多目標決策分析的科學性、準確性和可操作性。
其基本原理,是通過檢測評價對象與最優解、最劣解的距離來進行排序,若評價對象最靠近最優解同時又最遠離最劣解,則為最好;否則為最差。其中最優解的各指標值都達到各評價指標的最優值。最劣解的各指標值都達到各評價指標的最差值。
TOPSIS法中“理想解”和“負理想解”是TOPSIS法的兩個基本概念。所謂理想解是一設想的最優的解(方案),它的各個屬性值都達到各備選方案中的最好的值;而負理想解是一設想的最劣的解(方案),它的各個屬性值都達到各備選方案中的最壞的值。方案排序的規則是把各備選方案與理想解和負理想解做比較,若其中有一個方案最接近理想解,而同時又遠離負理想解,則該方案是備選方案中最好的方案。
TOPSIS法的數學模型[1]
遇到多目標最優化問題時,通常有m 個評價目標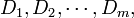 每個目標有n 評價指標
每個目標有n 評價指標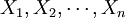 。首先邀請相關專家對評價指標(包括定性指標和定量指標) 進行打分,然後將打分結果表示成數學矩陣形式,建立下列特征矩陣:
。首先邀請相關專家對評價指標(包括定性指標和定量指標) 進行打分,然後將打分結果表示成數學矩陣形式,建立下列特征矩陣:
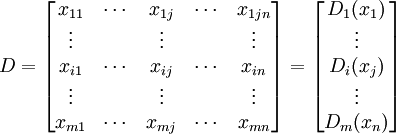
 。
。
計算規範化矩陣
對特征矩陣進行規範化處理,得到規格化向量rij ,建立關於規格化向量rij的規範化矩陣
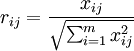
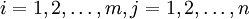 。
。
構造權重規範化矩陣
通過計算權重規格化值vij,建立關於權重規範 化值vij 的權重規範化矩陣
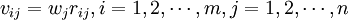 。
。
其中,wj是第j 個指標的權重。在基於ASP的動態聯盟製造資源評估模型中,採用的權重確定方法有Delphi法、對數最小二乘法、層次分析法、熵等。
確定理想解和反理想解
根據權重規格化值vij來確定理想解A * 和反理想解A − :
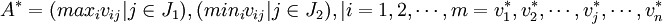 。
。
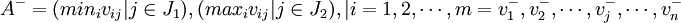 。
。
其中,J1是收益性指標集, 表示在第i個指標上的最優值; J2是損耗性指標集, 表示在第i個指標上的最劣值。收益性指標越大,對評估結果越有利;損耗性指標越小,對評估結果越有利。反之,則對評估結果不利。
計算距離尺度
計算距離尺度,即計算每個目標到理想解和反理想解的距離,距離尺度可以通過n維歐幾裡得距離來計算。目標到理想解A * 的距離為S * ,到反理想解A − 的距離為S − :
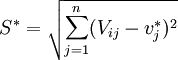
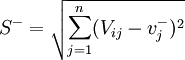
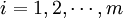 。
。
其中,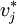 與
與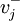 分別為第j個目標到最優目標及最劣目標的距離, vij是第i個目標第j個評價指標的權重規格化值。S * 為各評價目標與最優目標的接近程度, S * 值越小,評價目標距離理想目標越近,方案越優。
分別為第j個目標到最優目標及最劣目標的距離, vij是第i個目標第j個評價指標的權重規格化值。S * 為各評價目標與最優目標的接近程度, S * 值越小,評價目標距離理想目標越近,方案越優。
計算理想解的貼近度C *
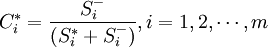 。
。
式中,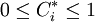 。當
。當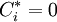 時, Ai = A − ,表示該目標為最劣目標;當
時, Ai = A − ,表示該目標為最劣目標;當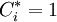 時, Ai = A * , 表示該目標為最優目標。在實際的多目標決策中, 最優目標和最劣目標存在的可能性很小。
時, Ai = A * , 表示該目標為最優目標。在實際的多目標決策中, 最優目標和最劣目標存在的可能性很小。
根據理想解的貼近度C * 大小進行排序
根據C * 的值按從小到大的順序對各評價目標進行排列。排序結果貼近度C * 值越大,該目標越優,C * 值最大的為最優評標目標。
- ↑ 李浩、羅國富、謝慶生.基於應用服務提供商的動態聯盟製造資源評估模型研究
評論(共5條)
不對,r是怎麼計算也沒寫
已添加r的計算公式,希望對您會有幫助!~
貼近度公式有誤吧,S*和S-的位置反了。 S*值越小,評價目標距離理想目標越近,方案越優的,如果按目前這個公式,S*=0時C*=0,成了最差方案了。
貼近度公式有誤吧,S*和S-的位置反了。 S*值越小,評價目標距離理想目標越近,方案越優的,如果按目前這個公式,S*=0時C*=0,成了最差方案了。
原文附有參考文獻,您可以做下對比,希望對您有幫助!








錯了!