格林定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
在物理學與數學中, 格林定理是指鏈接了一個封閉曲線上的線積分與一個邊界為C且平面區域為 D 的雙重積分。
格林定理是斯托克斯定理的二維特例,以英國數學家喬治•格林(George Green)命名。
設閉區域D由分段光滑的簡單曲線L圍成,函數P(x, y)及Q (x, y}在 D上具有一階連續偏導數,則有
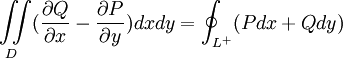
其中L是D的取正向的邊界曲線。格林公式還可以用來計算平面圖形的面積。
此公式叫做格林公式,它給出了沿著閉曲線C的曲線積分與C所包圍的區域D上的二重積分之間的關係。
以下是特殊情況下定理的一個證明,其中D是一種I型的區域,C2和C4是豎直的直線。對於II型的區域D,其中C1和C3是水平的直線。
如果我們可以證明
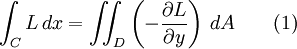
以及
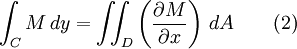
那麼就證明瞭格林公式是正確的。
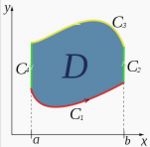
把右圖中I型的區域D定義為: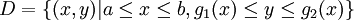 其中g1和g2是區間[a, b]內的連續函數。計算(1)式中的二重積分:
其中g1和g2是區間[a, b]內的連續函數。計算(1)式中的二重積分:
現在計算(1)式中的曲線積分。C可以寫成四條曲線C1、C2、C3和C4的並集。
對於C1,使用參數方程:x = x,y = g1(x),a ≤ x ≤ b。那麼:
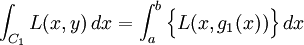
對於C3,使用參數方程:x = x,y = g2(x),a ≤ x ≤ b。那麼:
![\int_{C_3} L(x,y)\, dx = -\int_{-C_3} L(x,y)\, dx = - \int_a^b [L(x,g_2(x))]\, dx](/w/images/math/c/4/1/c414fd50f39dccb536e87c0519f773b6.png)
沿著C3的積分是負數,因為它是沿著反方向從b到a。在C2和C4上,x是常數,因此: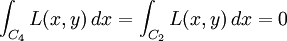
所以:
(3)和(4)相加,便得到(1)。類似地,也可以得到(2)。
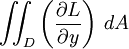
![=\int_a^b\!\!\int_{g_1(x)}^{g_2(x)} \left[\frac{\partial L (x,y)}{\partial y}\, dy\, dx \right]](/w/images/math/3/3/d/33d654ab5d0c1af5db56b9741638d931.png)
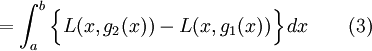
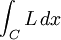
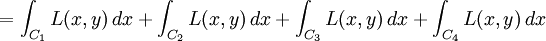
![= -\int_a^b [L(x,g_2(x))]\, dx + \int_a^b [L(x,g_1(x))]\, dx\qquad\mathrm{(4)}](/w/images/math/4/a/8/4a8ea1e07dac7011641487530c9167ee.png)







