格爾豐德-施奈德定理

出自 MBA智库百科(https://wiki.mbalib.com/)

格爾豐德-施奈德定理（Gelfond–Schneider theorem）

　　格爾豐德-施奈德定理是指一個可以用於證明許多數的超越數的結果。這個定理由Aleksandr Gelfond和Theodor Schneider在1934年獨立證明，它回答了希爾伯特第七問題。

　　如果α和β是代數數，其中α≠0且≠1，且β不是有理數，那麼任何α^β = exp{βlogα}的值一定是超越數。

　　α和β不限於實數；它們可以是複數。

　　一般地，α^β = exp{βlogα}是多值函數，其中“log”表示覆數對數。

　　該定理的一個等價的表述是：如果α和γ是非零的代數數，那麼(logγ) / (logα)要麼是有理數，要麼是超越數。

　　如果沒有β是代數數的限制，這個定理就不一定成立。例如，如果α = 3，β = log2 / log3，那麼α^β = 2，它是代數數。

　　利用這個定理，立刻就可以推出以下實數的超越性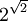：（格爾豐德-施奈德常數）和。

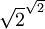　　e^π（格爾豐德常數），以及e^-π/2=iⁱ（這是因為是( − 1) ^{− i}的值之一）。