根軌跡法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　在時域分析中已經看到，控制系統的性能取決於系統的閉環傳遞函數，因此，可以根據系統閉環傳遞函數的零、極點研究控制系統性能。但對於高階系統，採用解析法求取系統的閉環特征方程根（閉環極點）通常是比較困難的，且當系統某一參數（如開環增益）發生變化時，又需要重新計算，這就給系統分析帶來很大的不便。

　　1948年，伊萬思根據反饋系統中開、閉環傳遞函數間的內在聯繫，提出了求解閉環特征方程根的比較簡易的圖解方法，這種方法稱為根軌跡法。因為根軌跡法直觀形象，所以在控制工程中獲得了廣泛應用。

　　根軌跡是當開環系統某一參數（如根軌跡增益 ）從零變化到無窮時，閉環特征方程的根在S平面上移動的軌跡。根軌跡增益K ^* 是首1形式開環傳遞函數對應的繫數。

　　在介紹圖解法之前，先用直接求根的方法來說明根軌跡的含義。控制系統如上圖所示。其開環傳遞函數為:

　　根軌跡增益 。閉環傳遞函數為:

　　閉環特征方程為:

　　特征根為：

　　當系統參數K ^* （或K）從零變化到無窮大時，閉環極點的變化情況見下表：

　　利用計算結果在S平面上描點並用平滑曲線將其連接，便得到K ^* （或K）從零變化到無窮大時閉環極點在S平面上移動的軌跡，即根軌跡，如下圖所示。圖中，根軌跡用粗實線表示，箭頭表示K ^* （或K）增大時兩條根軌跡移動的方向。

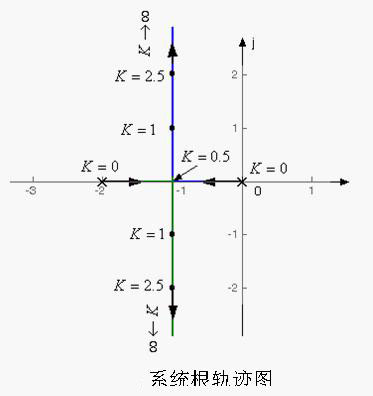
　　依據根軌跡圖（見系統根軌跡圖），就能分析系統性能隨參數（如K ^* ）變化的規律。

　　1．穩定性

　　開環增益從零變到無窮大時，如系統根軌跡圖所示的根軌跡全部落在左半s平面，因此，當K>0時，如圖控制系統根所示系統是穩定的；如果系統根軌跡越過虛軸進入右半s平面，則在相應K值下系統是不穩定的；根軌跡與虛軸交點處的K值，就是臨界開環增益。

　　2．穩態性能

　　由系統根軌跡圖可見，開環系統在坐標原點有一個極點，系統屬於Ⅰ型系統，因而根軌跡上的K值就等於靜態誤差繫數K_v。

　　當r(t)=1(t)時,　　e_ss = 0；

　　當r(t)=t時,　　

　　3．動態性能

　　由系統根軌跡圖可見，當0 < K < 0.5時，閉環特征根為實根，系統呈現過阻尼狀態，階躍響應為單調上升過程；

　　當K=0.5時，閉環特征根為二重實根，系統呈現臨界阻尼狀態，階躍響應仍為單調過程，但響應速度較0 < K < 0.5時為快；

　　當K>0.5時，閉環特征根為一對共軛復根，系統呈現欠阻尼狀態，階躍響應為振蕩衰減過程，且隨K增加，阻尼比減小，超調量增大，但t_s基本不變。

　　上述分析表明，根軌跡與系統性能之間有著密切的聯繫，利用根軌跡可以分析當系統參數（K）增大時系統動態性能的變化趨勢。用解析的方法逐點描畫、繪製系統的根軌跡是很麻煩的。我們希望有簡便的圖解方法，可以根據已知的開環零、極點迅速地繪出閉環系統的根軌跡。為此，需要研究閉環零、極點與開環零、極點之間的關係。

　　控制系統的一般結構如下圖所示，

　　相應開環傳遞函數為，假設

　　　　(1)

　　　　(2)

　　因此

　　　　(3)

　　式中，為系統根軌跡增益。對於m個零點、n個極點的開環系統，其開環傳遞函數可表示為

　　　　(4)

　　式中，Z_i表示開環零點，P_j表示開環極點。系統閉環傳遞函數為

　　　　(5)

　　由式（5）可見：

　　⑴閉環零點由前向通路傳遞函數G(s)的零點和反饋通路傳遞函數H(s)的極點組成。對於單位反饋系統H(s)=1，閉環零點就是開環零點。閉環零點不隨K ^* 變化，不必專門討論之。

　　⑵閉環極點與開環零點、開環極點以及根軌跡增益K ^* 均有關。閉環極點隨K ^* 而變化，所以研究閉環極點隨K ^* 的變化規律是必要的。

　　根軌跡法的任務在於，由已知的開環零、極點的分佈及根軌跡增益，通過圖解法找出閉環極點。一旦閉環極點確定後，再補上閉環零點，系統性能便可以確定。

　　閉環控制系統一般可用系統結構圖所示的結構圖來描述。開環傳遞函數可表示為

　　系統的閉環傳遞函數為

　　　　(6)

　　系統的閉環特征方程為

　　1 + G(s)H(s) = 0　　(7)

　　即

　　　　(8)

　　顯然，在s平面上凡是滿足式（8）的點，都是根軌跡上的點。式（8）稱為根軌跡方程。式（8）可以用幅值條件和相角條件來表示。

　　幅值條件：　　(9)

　　相角條件： 　　　　(10)

　　式中，、分別代表所有開環零點、極點到根軌跡上某一點的向量相角之和。

　　比較式（9）和（10）可以看出，幅值條件（9）與根軌跡增益K ^* 有關，而相角條件（10）卻與K ^* 無關。所以，s平面上的某個點，只要滿足相角條件，則該點必在根軌跡上。至於該點所對應的K ^* 值，可由幅值條件得出。這意味著：在s平面上滿足相角條件的點，必定也同時滿足幅值條件。因此，相角條件是確定根軌跡s平面上一點是否在根軌跡上的充分必要條件。

　　舉例：設開環傳遞函數為

　　其零、極點分佈如圖（系統開環零級點分佈圖）所示，判斷s平面上某點是否是根軌跡上的點。

　　解：在s平面上任取一點s₁，畫出所有開環零、極點到點s₁的向量，若在該點處相角條件

　　成立，則s₁為根軌跡上的一個點。該點對應的根軌跡增益K ^* 可根據幅值條件計算如下：

　　式中B，C，D分別表示各開環極點到s₁點的向量幅值，E表示開環零點到s₁點的向量幅值。

　　應用相角條件，可以重覆上述過程找到s平面上所有的閉環極點。但這種方法並不實用。實際繪製根軌跡是應用以根軌跡方程為基礎建立起來的相應法則進行的。

　　在控制系統的分析和綜合中，往往只需要知道根軌跡的粗略形狀。由相角條件和幅值條件所導出的8條規則，為粗略地繪製出根軌跡圖提供方便的途徑。

• 根軌跡的分支數等於開環傳遞函數極點的個數。
• 根軌跡的始點（相應於K=0）為開環傳遞函數的極點，根軌跡的終點（相應於K=∞）為開環傳遞函數的有窮零點或無窮遠零點。
• 根軌跡形狀對稱於坐標系的橫軸（實軸）。
• 實軸上的根軌跡按下述方法確定：將開環傳遞函數的位於實軸上的極點和零點由右至左順序編號，由奇數點至偶數點間的線段為根軌跡。
• 實軸上兩個開環極點或兩個開環零點間的根軌跡段上，至少存在一個分離點或會合點，根軌跡將在這些點產生分岔。
• 在無窮遠處根軌跡的走向可通過畫出其漸近線來決定。漸近線的條數等於開環傳遞函數的極點數與零點數之差。
• 根軌跡沿始點的走向由出射角決定，根軌跡到達終點的走向由入射角決定。
• 根軌跡與虛軸（縱軸）的交點對分析系統的穩定性很重要，其位置和相應的K值可利用代數穩定判據來決定。

　　在有些情況下，有必要對按基本規則畫出的根軌跡的粗略形狀，特別是位於虛軸附近的部分，進行修正，使之精確化。實現精確化的一條比較簡便的途徑，是採用一種由埃文斯設計的所謂對數螺旋尺的專用工具。

　　根軌跡的電腦輔助製圖,70年代以來，隨著電子電腦的普及，利用電腦對根軌跡的輔助製圖的演算法和程式都已建立，這大大減輕了系統分析和設計人員的繁重工作。

　　根軌跡的應用主要有三個方面。

　　1.用於分析開環增益(或其他參數)值變化對系統行為的影響：在控制系統的極點中，離虛軸最近的一對孤立的共軛複數極點對系統的過渡過程行為具有主要影響，稱為主導極點對。在根軌跡上，很容易看出開環增益不同取值時主導極點位置的變化情況，由此可估計出對系統行為的影響。

　　2.用於分析附加環節對控制系統性能的影響：為了某種目的常需要在控制系統中引入附加環節，這就相當於引入新的開環極點和開環零點。通過根軌跡便可估計出引入的附加環節對系統性能的影響。

　　3.用於設計控制系統的校正裝置：校正裝置是為了改善控制系統性能而引入系統的附加環節，利用根軌跡可確定它的類型和參數設計。