根轨迹法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　在时域分析中已经看到，控制系统的性能取决于系统的闭环传递函数，因此，可以根据系统闭环传递函数的零、极点研究控制系统性能。但对于高阶系统，采用解析法求取系统的闭环特征方程根（闭环极点）通常是比较困难的，且当系统某一参数（如开环增益）发生变化时，又需要重新计算，这就给系统分析带来很大的不便。

　　1948年，伊万思根据反馈系统中开、闭环传递函数间的内在联系，提出了求解闭环特征方程根的比较简易的图解方法，这种方法称为根轨迹法。因为根轨迹法直观形象，所以在控制工程中获得了广泛应用。

　　根轨迹是当开环系统某一参数（如根轨迹增益 ）从零变化到无穷时，闭环特征方程的根在S平面上移动的轨迹。根轨迹增益K ^* 是首1形式开环传递函数对应的系数。

　　在介绍图解法之前，先用直接求根的方法来说明根轨迹的含义。控制系统如上图所示。其开环传递函数为:

　　根轨迹增益 。闭环传递函数为:

　　闭环特征方程为:

　　特征根为：

　　当系统参数K ^* （或K）从零变化到无穷大时，闭环极点的变化情况见下表：

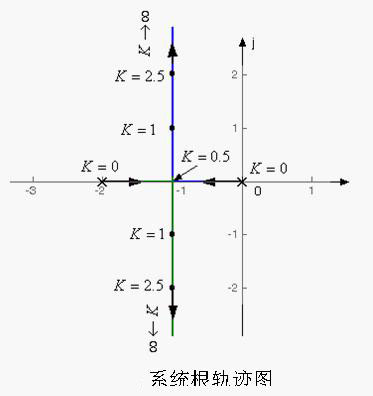
　　利用计算结果在S平面上描点并用平滑曲线将其连接，便得到K ^* （或K）从零变化到无穷大时闭环极点在S平面上移动的轨迹，即根轨迹，如下图所示。图中，根轨迹用粗实线表示，箭头表示K ^* （或K）增大时两条根轨迹移动的方向。

　　依据根轨迹图（见系统根轨迹图），就能分析系统性能随参数（如K ^* ）变化的规律。

　　1．稳定性

　　开环增益从零变到无穷大时，如系统根轨迹图所示的根轨迹全部落在左半s平面，因此，当K>0时，如图控制系统根所示系统是稳定的；如果系统根轨迹越过虚轴进入右半s平面，则在相应K值下系统是不稳定的；根轨迹与虚轴交点处的K值，就是临界开环增益。

　　2．稳态性能

　　由系统根轨迹图可见，开环系统在坐标原点有一个极点，系统属于Ⅰ型系统，因而根轨迹上的K值就等于静态误差系数K_v。

　　当r(t)=1(t)时,　　e_ss = 0；

　　当r(t)=t时,　　

　　3．动态性能

　　由系统根轨迹图可见，当0 < K < 0.5时，闭环特征根为实根，系统呈现过阻尼状态，阶跃响应为单调上升过程；

　　当K=0.5时，闭环特征根为二重实根，系统呈现临界阻尼状态，阶跃响应仍为单调过程，但响应速度较0 < K < 0.5时为快；

　　当K>0.5时，闭环特征根为一对共轭复根，系统呈现欠阻尼状态，阶跃响应为振荡衰减过程，且随K增加，阻尼比减小，超调量增大，但t_s基本不变。

　　上述分析表明，根轨迹与系统性能之间有着密切的联系，利用根轨迹可以分析当系统参数（K）增大时系统动态性能的变化趋势。用解析的方法逐点描画、绘制系统的根轨迹是很麻烦的。我们希望有简便的图解方法，可以根据已知的开环零、极点迅速地绘出闭环系统的根轨迹。为此，需要研究闭环零、极点与开环零、极点之间的关系。

　　控制系统的一般结构如下图所示，

　　相应开环传递函数为，假设

　　　　(1)

　　　　(2)

　　因此

　　　　(3)

　　式中，为系统根轨迹增益。对于m个零点、n个极点的开环系统，其开环传递函数可表示为

　　　　(4)

　　式中，Z_i表示开环零点，P_j表示开环极点。系统闭环传递函数为

　　　　(5)

　　由式（5）可见：

　　⑴闭环零点由前向通路传递函数G(s)的零点和反馈通路传递函数H(s)的极点组成。对于单位反馈系统H(s)=1，闭环零点就是开环零点。闭环零点不随K ^* 变化，不必专门讨论之。

　　⑵闭环极点与开环零点、开环极点以及根轨迹增益K ^* 均有关。闭环极点随K ^* 而变化，所以研究闭环极点随K ^* 的变化规律是必要的。

　　根轨迹法的任务在于，由已知的开环零、极点的分布及根轨迹增益，通过图解法找出闭环极点。一旦闭环极点确定后，再补上闭环零点，系统性能便可以确定。

　　闭环控制系统一般可用系统结构图所示的结构图来描述。开环传递函数可表示为

　　系统的闭环传递函数为

　　　　(6)

　　系统的闭环特征方程为

　　1 + G(s)H(s) = 0　　(7)

　　即

　　　　(8)

　　显然，在s平面上凡是满足式（8）的点，都是根轨迹上的点。式（8）称为根轨迹方程。式（8）可以用幅值条件和相角条件来表示。

　　幅值条件：　　(9)

　　相角条件： 　　　　(10)

　　式中，、分别代表所有开环零点、极点到根轨迹上某一点的向量相角之和。

　　比较式（9）和（10）可以看出，幅值条件（9）与根轨迹增益K ^* 有关，而相角条件（10）却与K ^* 无关。所以，s平面上的某个点，只要满足相角条件，则该点必在根轨迹上。至于该点所对应的K ^* 值，可由幅值条件得出。这意味着：在s平面上满足相角条件的点，必定也同时满足幅值条件。因此，相角条件是确定根轨迹s平面上一点是否在根轨迹上的充分必要条件。

　　举例：设开环传递函数为

　　其零、极点分布如图（系统开环零级点分布图）所示，判断s平面上某点是否是根轨迹上的点。

　　解：在s平面上任取一点s₁，画出所有开环零、极点到点s₁的向量，若在该点处相角条件

　　成立，则s₁为根轨迹上的一个点。该点对应的根轨迹增益K ^* 可根据幅值条件计算如下：

　　式中B，C，D分别表示各开环极点到s₁点的向量幅值，E表示开环零点到s₁点的向量幅值。

　　应用相角条件，可以重复上述过程找到s平面上所有的闭环极点。但这种方法并不实用。实际绘制根轨迹是应用以根轨迹方程为基础建立起来的相应法则进行的。

　　在控制系统的分析和综合中，往往只需要知道根轨迹的粗略形状。由相角条件和幅值条件所导出的8条规则，为粗略地绘制出根轨迹图提供方便的途径。

• 根轨迹的分支数等于开环传递函数极点的个数。
• 根轨迹的始点（相应于K=0）为开环传递函数的极点，根轨迹的终点（相应于K=∞）为开环传递函数的有穷零点或无穷远零点。
• 根轨迹形状对称于坐标系的横轴（实轴）。
• 实轴上的根轨迹按下述方法确定：将开环传递函数的位于实轴上的极点和零点由右至左顺序编号，由奇数点至偶数点间的线段为根轨迹。
• 实轴上两个开环极点或两个开环零点间的根轨迹段上，至少存在一个分离点或会合点，根轨迹将在这些点产生分岔。
• 在无穷远处根轨迹的走向可通过画出其渐近线来决定。渐近线的条数等于开环传递函数的极点数与零点数之差。
• 根轨迹沿始点的走向由出射角决定，根轨迹到达终点的走向由入射角决定。
• 根轨迹与虚轴（纵轴）的交点对分析系统的稳定性很重要，其位置和相应的K值可利用代数稳定判据来决定。

　　在有些情况下，有必要对按基本规则画出的根轨迹的粗略形状，特别是位于虚轴附近的部分，进行修正，使之精确化。实现精确化的一条比较简便的途径，是采用一种由埃文斯设计的所谓对数螺旋尺的专用工具。

　　根轨迹的计算机辅助制图,70年代以来，随着电子计算机的普及，利用计算机对根轨迹的辅助制图的算法和程序都已建立，这大大减轻了系统分析和设计人员的繁重工作。

　　根轨迹的应用主要有三个方面。

　　1.用于分析开环增益(或其他参数)值变化对系统行为的影响：在控制系统的极点中，离虚轴最近的一对孤立的共轭复数极点对系统的过渡过程行为具有主要影响，称为主导极点对。在根轨迹上，很容易看出开环增益不同取值时主导极点位置的变化情况，由此可估计出对系统行为的影响。

　　2.用于分析附加环节对控制系统性能的影响：为了某种目的常需要在控制系统中引入附加环节，这就相当于引入新的开环极点和开环零点。通过根轨迹便可估计出引入的附加环节对系统性能的影响。

　　3.用于设计控制系统的校正装置：校正装置是为了改善控制系统性能而引入系统的附加环节，利用根轨迹可确定它的类型和参数设计。