最小元素法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　最小元素法是找出運價表中最小的元素，在運量表內對應的格填入允許取得的最大數，若某行(列)的產量(銷量)已滿足，則把運價表中該運價所在行(列)划去；找出未划去的運價中的最小數值，按此辦法進行下去，直至得到一個基本可行解的方法。

　　註：應用西北角法和最小元素法，每次填完數，都只划去一行或一列，只有最後一個元素例外（同時划去一行和一列）。當填上一個數後行、列同時被滿足（也就是出現退化現象）時，也只任意划去一行（列）。需要填入“0”的位置不能任意確定，而要根據規則來確定。

　　所謂退化現象是指：當在平衡表中某一處填入一數字後，該數字所在的行和列同時被滿足，即需方的需求得到滿足，同時供方的供應數量也已經供完的現象。

　　最小元素法的基本思想是：運價最小的優先調運，即從單位運價中最小的運價開始確定供銷關係，然後次小，一直到給出初始基本可行解為止。

　　第一步：列出運價表和調運物資平衡表。

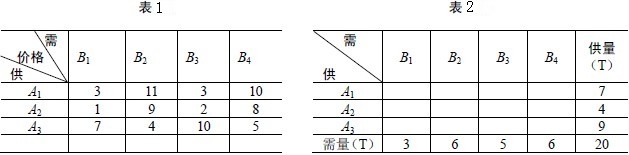
　　運用表上作業法時，首先要列出被調運物資的運價表和供需平衡表（簡稱平衡表），如表1，2所示。

　　第二步：編製初始調運方案。

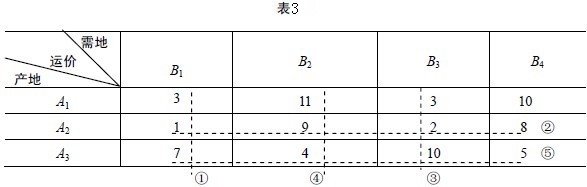
　　首先，在運價表中找出最小的數值(若幾個同為最小，則任取其中一個)，A₂B₁最小，數值為1，這表示先將A₂產品供應給B1 是最便宜的，故應給C₂₁所對應的變數x₂₁以盡可 能大的數值。顯然x₂₁=min{4,3}=3。在表4中的A₂B₁處填上“3”。B₁列被滿足，已不需要A₁和A₃再向它供貨，故運價表2中的第一列數字已不起作用，因此將原運價表1中的第一列划去，並標註①（見表3）。

　　然後，在運價表中未划去的元素中找最小運價A₂B₃ = 2，讓A₂ 儘量供應滿足B₃的需要，由於A₂的4已經供應了3T給B₁，最多只能供應1T給B₃。於是在平衡表的A₂B₃格中填上“1”；相應地由於A₂所生產的產品已全部供應完畢，因此，在運價表中與A₂ 同行的運價也不再起作用，所以也將它們划去，並標註②。

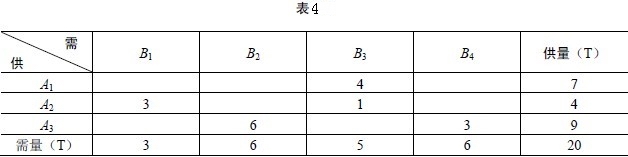
　　仿照上面的做法，一直做下去，就可以得到表4。

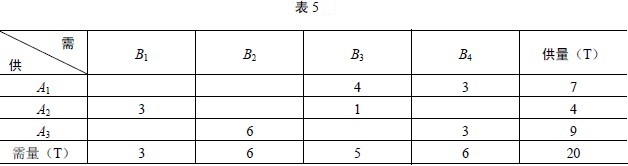
　　此時，在運價表中只有A₁B₄對應的運價10沒有劃掉，而B₄尚有3T需求，為了滿足供需平衡，所以最後在平衡表上對應A₁B₄處應填入“3”，這樣就得到表5。

　　對於編製初始方案說明以下幾點：應用最小元素法編製初始調運方案，這裡的“最小”系指局部而言，就整體考慮的運費不見得一定是最小的。可以作為初始方案的調運方案，其填有數字的方格數應是供應點個數加需求點個數之和再減1，即（m+n-1）。

　　第三步：初始方案的檢驗與調整。