度規函數

出自 MBA智库百科(https://wiki.mbalib.com/)

度規函數（Gauge Functions）

　　度規函數是指考慮兩產品的標準函數，該函數圖形是描述帶有生產前沿fr(P)的機會集合P。對於P內的任憊點x¹，如果能衡量其效率損失如何的低是有用的。即這一點離前沿多遠。這麼做的一種簡單方法，首先是要求出點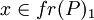。它正好是x¹的比例變化，對某個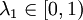,有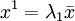。這樣，置J(x¹ | P) = λ₂，就定義了測定任意這樣的點相對於P的函數Jx¹ | P。為便它是有效的度量，它顯然應該具有這樣一種特性:當且僅當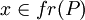就有J(x | P) = 1。

　　度規函數有二個類型：第1種，簡稱為度規函數，是對閔可夫斯基距離函數，而有時也叫作閔可夫斯基泛函的直接推廣。這種函數在數學中是常用的，但在經濟學中至今仍很少用，至少沒有明顯地用過。它們最適合位於原點附近的有界集合，諸如P以上部分以及麥肯齊的交易集合X_i。

　　第二種度規函數在數學中鮮為人知，但在經濟學中卻常常用到。它主要是對於不包括原點的無界集合而言的，諸如B^{t}以上部分和生產理論中的類似集合。經濟學家們給予這些函數許多命名，其中有“距離“函數、“變換”函數和“折縮”函數。

　　度規函數是數學凸分析的一個重要函數。設E為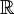或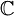上的矢量空間，有需要時可以假設為拓撲矢量空間。設C為在E內的凸集，且包含原點。那麼C的度規函數p是從E到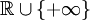的函數，定義為

　　,

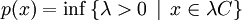　　如果C為空集，定義。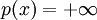

　　從定義立刻得到以下結果，可以進一步說明度規函數：

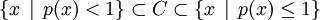
　　若C是在E中的開集，那麼；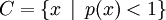

　　若C是在E中的閉集，那麼。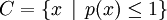

　　同樣地可立刻看出這條件當0是C的內點時成立。易證逆命題在有限維時成立：簡潔做法是看到p既是有限值和處處定義的凸函數，因而p連續，故此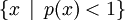包含在C內且是0的鄰域。

　　當0是在C的內部時，可以想象這樣一幅圖畫：函數取值1的點正好是凸集C的拓撲邊界，其他正數值的水平面是其位似形。如果有不在任一個水平面上的點，函數在該點取值為0。

　　最後再補充一點。在實矢量空間時，C相對0點對稱，其度規函數避開值，這度規函數便是半範數；在復矢量空間也有同樣結論，只需把對稱的定義，修改為與任何模為1的複數相乘都不變。

　　從定義看出度規函數在原點外一點x₀取0值，當且僅當從原點過x₀的射線包含在凸集內。

　　因此立刻可知在賦範矢量空間內，有界凸集的度規函數不在原點外取0值。

　　逆命題對有限維空間內的閉凸集成立，用半徑為1的球面的緊致性證明。