平均發展速度
出自 MBA智库百科(https://wiki.mbalib.com/)
平均發展速度(Average speed of development)
目錄 |
平均發展速度反映現象逐期發展速度的平均程度,是各個時期環比發展速度的幾何平均數,說明社會經濟現象在較長時期內速度變化的平均程度。
平均發展速度是一個十分重要並得到廣泛運用的動態分析指標,經常用來對比不同發展階段的不同發展速度,還用來對比不同國家或地區經濟發展的不同情況。
平均發展速度的計算有兩種方法:幾何平均法(水平法)和代數平均法(累計法或方程式法)。這兩種方法計算結果經常不一致,有時甚至會得出相反的結論。
設各個時期的發展水平為
a0 , a1 , a2 , a3 , …,an
平均發展速度的計算公式為
![\bar{v}=\sqrt[n]{\frac{a_1}{a_0}\times\frac{a_2}{a_1}\times\ldots\times\frac{a_n}{a_{n_1}}}](/w/images/math/3/a/f/3af7a842d500dbf68eadf79ec4272999.png)
或者
平均發展速度![\bar{v}=\sqrt[n]{v_1\times v_2\times\ldots\times v_n}](/w/images/math/e/3/f/e3f1e7eca8e9a0d1c6da812a1ea8c6e5.png)
一、兩種計算方法的比較分析
幾何平均法和代數平均法的區別主要有:
(一)、依據的基礎數據及計算公式不同。幾何平均法的理論基礎是:平均發展速度是總速度的平均,但現象發展的總速度,不等於各期發展速度之和,而等於各期環比發展速度的連乘積。而一段時期的 定基發展速度即為現象的總速度。因而幾何平均法直接用各期環比發展速度的連乘積等於定基發展速度的關係,得出平均發展速度的計算公式:
![\bar{x}=\sqrt[n]{x_1\times x_2\times \ldots x_n}](/w/images/math/f/2/2/f22371c8782a399beadd6b5406ceb7c9.png)
或 ![\bar{x}=\sqrt[n]{\frac{a_1}{a_0}\times\frac{a_2}{a_1}\times\ldots\times\frac{a_n}{a_{n-1}}}=\sqrt[n]{\frac{a_n}{a_0}}](/w/images/math/d/3/7/d37abec79d3e546ba6c5beaca53abbbc.png)
式中: 表示平均發展速度;xi(i=0,1,2…n)表示各期環比發展速度;n表示環比發展速度的項數;ai (i=0,1,2…n)表示各期發展水平。
表示平均發展速度;xi(i=0,1,2…n)表示各期環比發展速度;n表示環比發展速度的項數;ai (i=0,1,2…n)表示各期發展水平。
代數平均法是基於時間數列各期發展水平之和等於累計發展水平,以累計發展水平與基期水平之比為基礎來計算的。計算公式為:
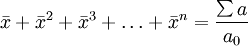
這個方程式的正根,即為平均發展速度。
式中: 表示平均發展速度;Σa表示累計發展水平;a0表示基期水平。
表示平均發展速度;Σa表示累計發展水平;a0表示基期水平。
(二)、側重點不同。幾何平均法側重於考察最末一期的發展水平,按這種方法所確定的平均發展速度推算的最末一期發展水平,等於最末一期的實際水平;而推 算的最末一期的定基發展速度,和實際數據的定基發展速度一致。代數平均法則側重於考察全期各期的發展水平之和,按這種方法所確定的平均發展速度推算的全期 各期發展水平的總和,與全期各期實際數據總和一致;而推算的各期定基發展速度的總和,與實際數據的定基發展速度的總和也是一致的。
(三)、影響因素不同。用幾何平均法計算,其平均發展速度只受最末水平(an)和最初水平(a0)的影響,不受中間水平的影響。用代數平均法計算,其平均發展速度受時間數列中所有發展水平的影響,即既受最末水平(an)和最初水平(a0)的影響,也受中間水平的影響。
(四)、計算結果不同,有時甚至會得出相反的結論。
例如,甲地區“十五”時期糧食產量資料如表1所示:
表1 甲地區“十五”時期糧食產量 單位:萬噸
年 份 2000(基期) 2001 2002 2003 2004 2005 糧食產量(萬噸) 100 106 104 108 110 92
按幾何平均法計算“十五”時期的平均發展速度為:
![\bar{x}=\sqrt[n]{\frac{a_n}{a_0}}=\sqrt[5]{\frac{92}{100}}=98.35%](/w/images/math/3/8/0/380fd7795a0aefe6b4aefa52ff321bc9.png)
按代數平均法計算“十五”時期的平均發展速度為:
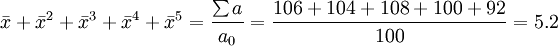
查“平均增長速度累計法查對錶—遞增速度”得 =101.3%
以上計算結果表明,同樣的資料,採用不同的計算方法,會得出相反的結論。甲地區按幾何平均法計算,平均發展速度降低率為1.65%;而按代數平均法計算,平均發展速度增長率為1.3%。
=101.3%
以上計算結果表明,同樣的資料,採用不同的計算方法,會得出相反的結論。甲地區按幾何平均法計算,平均發展速度降低率為1.65%;而按代數平均法計算,平均發展速度增長率為1.3%。
二、兩種計算方法的選擇
當兩種計算方法的結果出現相反的結論時,最好選擇代數平均法。理由如下:
(一)、從經濟意義上考慮。在基期水平既定的情況下,代數平均法的計算結果取決於累計發展水平(Σa),在觀察長時間內經濟指標的變動時,累計發展水平可以說明社會經濟的總成果,有現實的經濟意義。而幾何平均法的計算結果則取決於最末水平(an),當最末水平由於社會因素、自然因素等出現偶然波動時,用幾何平均法計算的平均發展速度就會失真,沒有實際經濟意義。
(二)、從公式本身考慮。代數平均法按時間數列全期發展水平之和與基期水平對比去計算,計算結果準確性高。而幾何平均法只按時間數列最末水平與最初水平對比去計算,中間各期的水平儘管也是組成時間數列的重要部分,卻不參與計算,因而平均發展速度的計算結果準確性差。
(三)、從平均發展速度的代表性考慮。
雖然用幾何平均法和代數平均法求得的平均發展速度均是各期環比發展速度的代表值,但代表性大小卻不相同。現以上述甲地區的資料為例,計算推算值和實際值的離差及估計標準誤,見表2:
表2 甲地區糧食產量的推算水平及離差計算表 單位:萬噸
年份 實際水平 按幾何平均法計算 按代數平均法計算 推算的發展水平 實際水平與推算水平離差 推算的發展水平 實際水平與推算水平離差 2000(基期) 100 100 0 100 0 2001 106 98.4 7.6 101.3 4.7 2002 104 96.7 7.3 102.6 1.4 2003 108 95.1 12.9 104 4 2004 110 93.6 16.4 105.3 4.7 2005 92 92 0 106.7 -14.7
幾何平均法下的離差和=Σ(y-yc)=7.6+7.3+12.9+16.4+0=44.2(萬噸)
幾何平均法下的估計標準差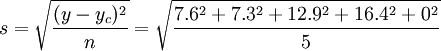 =10.45(萬噸)
=10.45(萬噸)
代數平均法下的離差和=Σ(y-yc)= 4.7+1.4+4+4.7-14.7=0.1(萬噸)
代數平均法下的估計標準差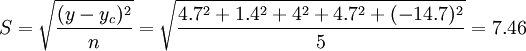 (萬噸)
(萬噸)
從上述計算可知,用代數平均法法推算的各期發展水平與實際水平的離差之和接近於0,這很符合算術平均數的性質。上述計算結果表明,無論是推算水平與實際水平 的離差之和,還是估計標準誤差,用代數平均法計算都比用幾何平均法計算要小,這說明用代數平均法計算的平均發展速度代表性高。
(四)、從適用範圍考慮。
用幾何平均法計算的平均發展速度只適用於環比發展速度大致相等的時間數列。因為在測定時間數列長期趨勢時,若各時期環比發展速度大致相等,應配合指數曲線方程(y = abx),這一方程中的y相當於最末水平(an),a相當於最初水平(a0),b相當於平均發展速度( ),x相當於時間(n),即
),x相當於時間(n),即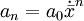 。 但當時間數列的逐期增長量大致相等或二級增長量大致相等時,用幾何平均法計算平均發展速度就不合適。因為時間數列的逐期增長量大致相等,應配合直線方程, 二級增長量大致相等時,應配合拋物線方程。而按代數平均法計算的平均發展速度是基於時間數列全期的發展水平,因此,適用於各種類型的時間數列。
。 但當時間數列的逐期增長量大致相等或二級增長量大致相等時,用幾何平均法計算平均發展速度就不合適。因為時間數列的逐期增長量大致相等,應配合直線方程, 二級增長量大致相等時,應配合拋物線方程。而按代數平均法計算的平均發展速度是基於時間數列全期的發展水平,因此,適用於各種類型的時間數列。








好,有沒有平均增長速度