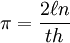布豐投針問題

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

布豐投針問題（Buffon neddle ）

什麼是布豐投針問題

　　布豐投針問題是指18世紀布豐提出的問題：設我們有一個以平行且等距木紋鋪成的地板（如圖），現在隨意拋一支長度比木紋之間距離小的針，求針和其中一條木紋相交的概率。

[編輯]

布豐投針問題的解法

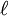　　設針的長度是 $\ell$ ，並行線之間的距離為 $t$ ， $x$ 為針的中心和最近的並行線的距離， $θ$ 為針和線之間的銳角。

　　 $x \in [0,t/2]$ 的機率密度函數為 $\frac{2}{t}dx$ 。

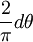　　 $\theta \in [0,\pi/2]$ 的機率密度函數為 $\frac{2}{\pi}d\theta$ 。

　　 $x,θ$ 兩個隨機變數互相獨立，因此兩者結合的機率密度函數只是兩者的乘法|積：

$\frac{4}{t\pi}dxd\theta$ 。

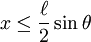　　當 $x \le \frac{\ell}{2}\sin\theta$ ，針和線相交。

　　求上式的積分，得針與線相交的機率：

$\int_0^{\frac{\pi}{2}} \int_0^{(\ell/2)\sin\theta} \frac{4}{t\pi}dxd\theta = \frac{2\ell}{t\pi}.$

　　拋 $n$ 支針，其中有 $h$ 支針與線相交的機率是：

$\frac{h}{n} = \frac{2\ell}{t\pi},$

　　由此可求得π：

$\pi = \frac{2\ell n}{th}$

[編輯]

布豐投針問題的相關實驗

　　1901年義大利數學家Mario Lazzarini嘗試進行此實驗。他拋了3408次針，得到π的近似值為355/113。

　　Lazzarini選取了一支長度是紋的距離的5/6的針。在這個情況，針和紋相交的機會是5/(3π)。如果想拋n次針而得到x次相交，π約等於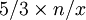 $5/3 \times n/x$ 。分母、分子少於五位數字，沒有比355/113更好的π的近似值了。因此，可以列式 $355/113 = 5/3 \times n/x$ ，得 $x = 113 n / 213$ 。