完全消耗繫數

出自 MBA智库百科(https://wiki.mbalib.com/)

　　概括地說，指某一部門單位最終使用需要完全消耗各部門貨物和服務的價值量。

　　具體地說，完全消耗繫數是指第j產品部門每提供一個單位最終使用時，對第i產品部門貨物或服務的直接消耗和間接消耗之和。

　　將各產品部門的完全消耗繫數用表的形式表現出來，就是完全消耗繫數表或完全消耗繫數矩陣，通常用字母Ｂ表示。完全消耗繫數的計算公式為：

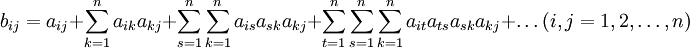
　　式中的第一項a_ij表示第j產品部門對第i產品部門的直接消耗量；式中的第二項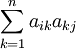表示第j產品部門對第i產品部門的第一輪間接消耗量；式中的第三項為第二輪間接消耗量；式中的第四項為第三輪間接消耗量；依此類推，第n+1項為第n輪間接消耗量。按照公式所示，將直接消耗量和各輪間接消耗量相加就是完全消耗繫數。

　　完全消耗繫數矩陣可以在直接消耗繫數矩陣的基礎上計算得到的，利用直接消耗繫數矩陣計算完全消耗繫數矩陣的公式為：

　　B = (I − A) ^{− 1} − I

　　式中的A為直接消耗繫數矩陣，I為單位矩陣，B為完全消耗繫數矩陣。

　　完全消耗繫數不僅反映了國民經濟各部門之間直接的技術經濟聯繫，還反映了國民經濟各部門之間間接的技術經濟聯繫，並通過線性關係，將國民經濟各部門的總產出與最終使用聯繫在一起。

• 直接消耗繫數