太古奇損失函數
出自 MBA智库百科(https://wiki.mbalib.com/)
太古奇損失函數(The Taguchi Quality Loss Function)
目錄 |
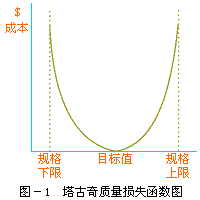
顧客追求的是價值的最大化。賴恩·L·喬依納博士在《第四代管理》中,利用顧客損失函數來測量顧客的價值。太古奇博士提出:離目標越遠,損失越大。人們可以通過越來越接近目標,來減少損失。如果用橫坐標Y表示顧客所需要的產品或服務的特性值;用m表示顧客確定的價值最大化的目標值;q(y)表示顧客損失函數。那麼從圖上可以看出,當質量特征值y離目標值m越遠,顧客的損失就越大;當y=m時,顧客價值達到最大化。
比如一個住在飯店的顧客,要求飯店每天早上7點送飯,並告訴飯店,如果遲送6分鐘可能影響他的其他工作安排,將造成經濟損失10元,則本例中m=7點,當y=7.1點時q(y)=10元,依據損失函數的數學推導可得q(y)=k(y-m) ,其中k是不依賴y的常數,則: 10=k(7.1-7) ,其中k=10/(0.1) =1000;現若飯店遲送15分鐘,則顧客可能損失q(y)=1000×(7.25-7) =62.50元,當然飯店可制定一個目標範圍界限,6:50-7:10分是送飯時間,但若顧客有特殊要求時,則必須服從顧客的需要。如果是產品也同樣可以計算出偏離顧客確定的損失最小的目標值時顧客將可能受到的損失。
損失函數可表示為:L(y) = K(y − T)2
其中:K為外部故障成本結構的比例常數;
y為質量特征的實際值;
T為質量特征的目標值;
L為質量損失。
示例:假設K=200,T=5cm,4件產品的質量損失計算如表:
單 位 實際直徑(y) y-T (y − T)2 K(y − T)2 1 4.9㎝ -0.10 0.01 2.00元 2 5.1㎝ 0.10 0.01 2.00元 3 5.2㎝ 0.20 0.04 8.00元 4 4.8㎝ -0.20 0.04 8.00元 總 數 0.10 20.00元 平均數 0.025 5.00元
評析:計算的平均數(包括平均方差和單位平均損失)可用來計算某種產品的總預期隱性質量成本。例如,如果生產產品總量為1 000件,平均方差為0.025,則每單位的預期成本為5元(0.025×200),1 000件產品的總預期損失為5 000元(5×1 000)。
運用此函數的關鍵在於估計K值。K值是通過將某一規格界限外的估計成本除以該界限偏離目標值的方差計算而得,即:K = C / d2。
其中:C為規格上限或下限處的損失;
d為界限與目標值的距離。
值得指出的是,還可以用乘數法與市場研究法來估計K值。
損失是相對於目標而言的,那麼顧客的損失是企業提供給顧客的並被顧客所感知的與顧客預先的期望比較之後的差異。該模型中的損失是一個絕對值的概念,只要偏離顧客原先訂立的目標,就會給顧客帶來損失。但是,我們應該看到,損失其實應有正向損失和負向損失之分,如果企業提供給顧客並被其感知的部分小於顧客的目標,這種差距可以稱之為正向損失;反之,則稱為負向損失。負向損失可以理解為是顧客事先沒有預想到的,不在顧客期望的範圍內,可一旦出現在顧客面前,顧客就會驚喜地發現:“這正是我想要的,為什麼我一直沒發現呢!”這種負向的損失實際上增加了顧客的價值,而不是損失。若按照這一模型,我們不難推導出:超出顧客期望部分的“損失”是不可取的,它使得顧客價值減少了。顯然,與事實是不符的。








好