雙線性插值

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

雙線性插值(Bilinear interpolation)

什麼是雙線性插值

　　雙線性插值又稱為雙線性內插.在數學上，雙線性插值是有兩個變數的插值函數的線性插值擴展，其核心思想是在兩個方向分別進行一次線性插值。

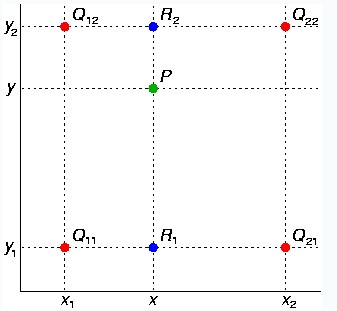
　　紅色的數據點與待插值得到的綠色點假如我們想得到未知函數f在點P=(x,y)的值，假設我們已知函數f在 $Q 11 = (x 1, y 1)$ 、 $Q 12 = (x 1 . y 2), Q 21 = (x 2, y 1)$ 以及 $Q 22 = (x 2, y 2)$ 四個點的值。

　　首先在x方向進行線性插值，得到

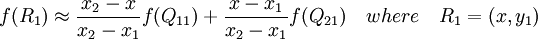
　　 $f(R_1)\approx\frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})\quad where\quad R_1=(x,y_1)$

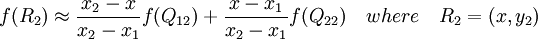
　　 $f(R_2)\approx\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})\quad where\quad R_2=(x,y_2)$

　　然後在y方向進行線性插值，得到

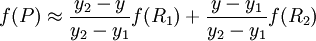
　　 $f(P)\approx\frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2)$

　　這樣就得到所要的結果f(x,y)，

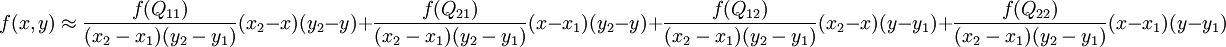
　　 $f(x,y)\approx\frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y_2-y)+\frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y_2-y)+\frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y-y_1)+\frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y-y_1)$

　　如果選擇一個坐標系統使得f的四個已知點坐標分別為(0,0)、(0,1)、(1, 0) 和 (1, 1)，那麼插值公式就可以化簡為

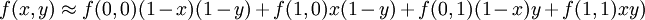
　　 $f(x,y)\approx f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy)$

　　或者用矩陣運算表示為

　　 $f(x,y)\approx\left[1-x\quad x\right]\begin{bmatrix}f(0,0)&f(0,1)\\f(1,0)&f(1,1)\end{bmatrix}\begin{bmatrix}1-y\\y\end{bmatrix}$

　　與這種插值方法名稱不同的是，這種插值方法並不是線性的，它的形式是

　　 $(a 1 x + a 2)(a 3 y + a 4)$

　　它是兩個線性函數的乘積。另外，插值也可以表示為

　　 $b 1 + b 2 x + b 3 y + b 4 x y$

　　在這兩種情況下，常數的數目]都對應於給定的f的數據點數目。

　　線性插值的結果與插值的順序無關。首先進行y方向的插值，然後進行x方向的插值，所得到的結果是一樣的。

　　雙線性插值的一個顯然的三維空間延伸是三線性插值。

[編輯]

本条目由以下用户参与贡献

Yixi.

頁面分類: 應用數學

評論(共2條)

提示:評論內容為網友針對條目"雙線性插值"展開的討論，與本站觀點立場無關。

123.235.4.* 在 2011年1月18日 16:49 發表

這裡面是不是有錯誤呀。

回複評論

Yixi (討論 | 貢獻) 在 2011年1月19日 11:50 發表

123.235.4.* 在 2011年1月18日 16:49 發表

這裡面是不是有錯誤呀。

感謝您的指正，原文已修正。

回複評論

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

雙線性插值

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是雙線性插值

相關條目

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共2條)

導航

意见反馈

查看

工具▼

雙線性插值

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是雙線性插值

相關條目

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共2條)

導航

意见反馈