單純移動平均法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是單純移動平均法[1]
單純移動平均法是指將事件過去若幹相關期發生的實際觀察值,按時間序列排列,然後,由遠而近按一定的跨越期數一組一組地逐一地求得其算術平均值,將每一次計算的平均值向下移動—個時間單位,即可直接作為下一個時間單位(期)的預測值。
單純移動平均法的公式[1]
其計算公式是:
式中:
yt第t期的移動平均值,直接作為t+1期的預測值;
t——觀察期(資料規的序列數;
si——第i期的實際觀察值;
n——跨越期數,也叫移動資料期數。
跨越期數n如何確定?一般地說,應取同預測期相鄰且有密切關係的若幹期。通常,當資料數據的波動較大時,n應取小一點,反之,n可以取小一點。
當需要連續計算多組移動平均值時、且所取跨越期數又較多時,對上式加以改寫將帶來許多方便。
我們將上式展開:
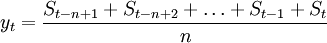
則
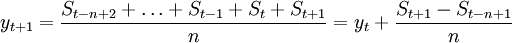
於是,也可以如下算式:
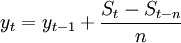
這樣,如果我們已經求得了前一期的移動平均值;便可很方便地求得後一期的移動平均值。反之,也可利用後一期的移動平均值去求前一期的移動平均值。
單純移動平均法分析[1]
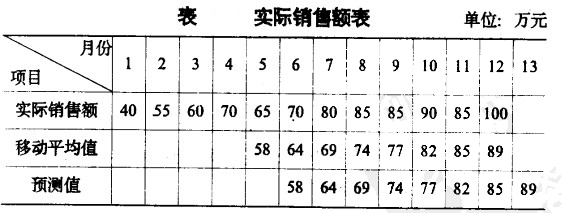
某企業過去12個月的實際銷售額如表所示,假設計算所用跨越期數為n=5,現計算各個移動平均值,並作預測。
首先,計算5月份的移動平均值
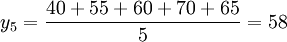 (萬元)
(萬元)
其餘類推,便可求得5-12月的移動平均值。將這些移動平均值分別向下移動一個時間單位(月),即可求得下一個時間單位(月)的預測值。如表所示。例如,第12個月的預測銷售額為85萬元。第13個月的預測銷售額為89萬元。
另外,這種方法是以實際觀察值為依據,因而,只能用於實際觀察值序列的緊後期,而無法預測相隔若幹期後的事件;還有,這種方法所求得的預測值受所取跨越期數的影響,如上例中,若取跨越期數n=8,第13個月的預測銷售額就成為82.5萬元,而不再是89萬元了。
單純移動平均法的優缺點[1]
單純移動平均法的優點是簡單易行,且可在一定程度上消除某些偶然因素的影響。
但它也存在著比較明顯的缺點:由於這種方法直接將第t期的移動平均值作為第t-1期的預測值,因而當實際觀察值的時間序列具有明顯的變化趨勢時,預測值就會出現滯後於這種趨勢的現象(如上例);
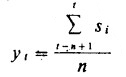








好厲害