動載荷

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

動載荷(Dynamic Load)

什麼是動載荷^[1]

　　動載荷是指隨時間作明顯變化的載荷，即具有較大載入速率的載荷。

[編輯]

動載荷產生的原因^[2]

　　工程實際中常見的動載荷一般產生於以下幾個原因：

　　(1)加速度引起的動載荷

　　例如起重機加速起吊重物時，吊索受到因加速度而產生的附載入荷作用；飛輪作勻速轉動時因法向加速度而使輪緣受到附載入荷作用。

　　(2)衝擊載荷或突載入荷

　　這種載荷的特點是在極短的時間內將載荷加在被衝擊的構件上，例如錘對樁的衝擊力，炸葯對物體的爆破力等。衝擊載荷對構件的作用力遠遠大於靜載荷。

　　(3)振動載荷

　　這種載荷的特點是其大小和方向都隨時間作周期性變化，例如機器中具有偏心質量的轉動部分在運轉時對廠房及其基礎的作用力。

[編輯]

動載荷繫數^[3]

　　(1)運行衝擊繫數 $α 1$

　　起重機或小車通過不平道路或軌道接縫時的鉛垂方向的衝擊效應。在考慮這種工況的載荷組合時，應將自重載荷和起升載荷乘以運行衝擊繫數。運行衝擊繫數與起重機或小車的運行速度、軌道或道路狀況有關。運行衝擊繫數可按下式計算。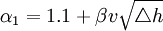 $\alpha_1=1.1+\beta v\sqrt{\triangle h}$

　　式中　　v——運行速度，m／s；

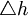　　　　　　 $\triangle h$ ——軌道接縫處兩軌道面的高度差，mm；

　　　　　　 $β$ ——經驗繫數， $β = 0.058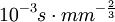$ ， $10^{-3}s\cdot mm^{-\frac{2}{3}}$ 。

　　(2)起升衝擊繫數 $α 2$

　　起升質量突然離地起升或下降制動時，自重載荷將產生沿其加速度相反方向的衝擊作用。在考慮這種工況的載荷組合時，起升衝擊繫數與起重機自重載荷相乘。

α 2

的數值範圍如下。0．9≤

α 2

≤1．1

　　(3)起升載荷動載繫數 $α 3$

　　起升質量突然離地起升或下降制動時，考慮被弔物品重力的動態效應的起升載荷增大繫數。在考慮這種工況的載荷組合時，起升載荷動載繫數與起升載荷相乘。

α 3

值的大小與起升速度、系統剛度及操作情況有關，一般在1．0～2．0範圍內。起升速度越大，系統剛度越大，操作越猛烈，則

α 3

值也越大。

α 3

值可用如下公式估算。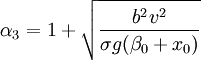 $\alpha_3=1+ \sqrt{\frac{b^2v^2}{\sigma g(\beta_0+x_0)}}$

　　式中　　b——操作繫數， $b = v 0 / v$ ；

　　　　　　 $v 0$ ——起升質量離地瞬間的起升速度，m／s；

　　　　　　v——額定起升速度，m／s；

　　　　　　σ——結構質量影響繫數；

　　　　　　g——重力加速度，m／ $s 2$ ；

　　　　　　 $β 0$ ——在額定起升載荷作用下，下滑輪組對上滑輪組的位移量，m；

　　　　　　 $x 0$ ——在額定起升載荷作用下物品懸掛處的結構靜變位移，m。

　　(4)突然卸荷衝擊繫數 $α 4$

　　當起升質量部分或全部突然卸載時，將對結構產生動態減載作用。這種工況對金屬結構和起重機抗傾覆的穩定性計算非常有用。減小後的起升載荷等於突然卸載的衝擊繫數與起升載荷的乘積。

α 4

值可用如下公式估算。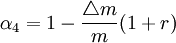 $\alpha_4=1-\frac{\triangle m}{m}(1+r)$

　　式中　　r——起重機的繫數，對於電磁起重機或類似的起重機，r=1.0；對於抓鬥起重機或

　　　　　　類似起重機，r=0．5；

　　　　　　△m——起升質量中突然卸去的那部分質量，kg；

　　　　　　m——起升質量，kg。

[編輯]

動載荷計算的基本方法^[4]

　　1．物體作一般加速度時的動荷問題

　　慣性力與動靜法　　作加速度運動物體的慣性力大小等於物體的質量m和加速度a的乘積，方向與a相反。假想在每一具有加速度的運動質點上加上慣性力，則物體(質點系)上作用的原力系與慣性力系將組成平衡力系。這樣就可以把動力問題在形式上作為靜力學問題來處理，這就是達朗伯原理。此時物體(構件)的許用應力仍然取靜荷強度。

　　2．衝擊問題

　　(1)衝擊問題的力學模型

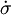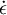　　衝擊問題的特點是構件內材料質點在極短時間內承受速度很大的載荷，獲得很大的 $\dot{\sigma}$ 和 $\dot{\epsilon}$ 。這是一個非常複雜的能量傳遞、轉化和耗散過程。工程上採用偏於保守的能量平衡方程來近似估算被衝擊物所受衝擊載荷與衝擊應力。它把衝擊物與受衝擊物(構件)簡化為一個質量與一個彈簧構成的衝擊系統並略去衝擊過程中聲、熱、振動等的能量傳遞與耗散。

　　(2)衝擊系統的能量平衡方程

　　對上述力學模型，按照機械能守恆定律，對衝擊系統可寫出能量平衡方程

T i + V i + U i = T d + V d + U d

　　(1) 此處下標i表示衝擊物與受衝擊構件發生衝擊前那一瞬時

t i

的各量。下標d為衝擊過程結束那一瞬時

t f

的各量，

t f

瞬時受衝擊構件達到最大衝擊變形含

δ d

。

T i, V i, U i

為

t i

瞬時系統的動能、重力勢能和彈性變形能。

T d, V d, U d

為

t f

瞬時系統的動能、重力勢能和彈性變形能。對上述衝擊系統的力學模型有以下補充假設：①衝擊過程中衝擊物無回彈、無變形；②受衝擊構件的質量可以略去不計，在衝擊過程中它的動變形與衝擊載荷服從胡克定律。當動變形達到最大值

δ d

時，衝擊載荷也達到最大值

Q d

，且與靜載荷Q、靜變形

δ s t

，靜應力

σ s t

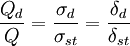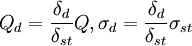，有以下關係 $\frac{Q_d}{Q}=\frac{\sigma_d}{\sigma_{st}}=\frac{\delta_d}{\delta_{st}}$ 　　或　　 $Q_d=\frac{\delta_d}{\delta_{st}}Q,\sigma_d=\frac{\delta_d}{\delta_{st}}\sigma_{st}$ 　　(2)

　　(3)衝擊能量平衡方程對自由落體衝擊問題的應用

　　圖1所示為重量Q的物體從高h處自由下落衝擊彈簧。設

t f

瞬時彈簧具有最大彈性變形

δ d

，相應有最大衝擊載荷

Q d

，衝擊功

W d

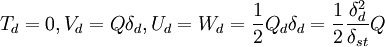
，則知 $V_i=0,U_i=0,T_i=\frac{1}{2}\frac{Q}{g}v^2=\frac{1}{2}\frac{Q}{g}\cdot 2gh=Qh$ $T_d=0,V_d=Q\delta_d,U_d=W_d=\frac{1}{2}Q_d\delta_d=\frac{1}{2}\frac{\delta_d^2}{\delta_{st}}Q$ 　　代入式(1)簡化後可得以

δ d

或

Q d

為變數的能量平衡方程，如以

δ d

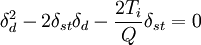
為變數則有 $\delta_d^2-2\delta_{st}\delta_d-\frac{2T_i}{Q}\delta_{st}=0$ 可解得

δ d = K d δ s t, P d = K d Q,σ d = K d σ s t

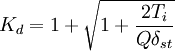　　(3) 其中衝擊動荷繫數 $K_d=1+\sqrt{1+\frac{2T_i}{Q\delta_{st}}}$ 　　(4a) 如果

T i

由重物自由落體產生，有

T i = Q h

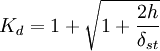，則 $K_d=1+\sqrt{1+\frac{2h}{\delta_{st}}}$ 　　(4b)

　　3．受迫振動的動應力

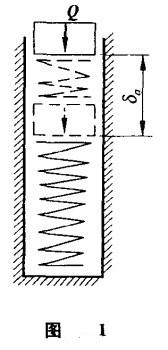
　　構件(梁、桿、軸等)在周期性變化的干擾力作用下作受迫振動的力學模型如圖2所示，這一質量—彈簧系統中，重物簡化為質量為m的質點，構件簡化為剛度為C的彈簧，質點在以下諸力作用下作受迫振動：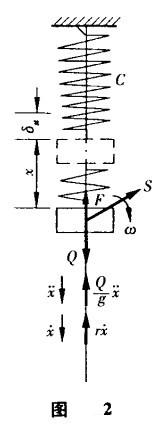

　　(1)干擾力S　　設按正弦規律變化，S＝Hsinωt，H為干擾力幅值(最大值)，ω為角頻率，ωt是相位；

　　(2)重物(質點)重力Q　　略去構件(彈簧)質量；

　　(3)彈簧恢復力F　　F＝C( $δ s t$ +x)， $δ s t$ 為彈簧在Q作用下的靜位移，x為質點在振動瞬時的位置；

　　(4)阻力R　　R＝r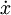 $\dot{x}$ ，r為阻尼的阻力繫數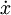， $\dot{x}$ 為質點的運動速度；

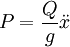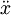　　(5)質點慣性為P　　 $P=\frac{Q}{g}\ddot{x}$ ， $\ddot{x}$ 為質點的運動加速度。由此寫出振動系統的運動方程，簡化後為 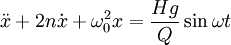$\ddot{x}+2n\dot{x}+\omega_0^2x=\frac{Hg}{Q}\sin \omega t$ 　　(5) n為阻尼繫數，n＝gr／(2Q)；

ω 0

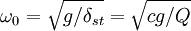為彈性系統的固有頻率， $\omega_0=\sqrt{g/\delta_{st}}=\sqrt{cg/Q}$ 。微分方程(5)通解

x = x 1 + x 2

，

x 1

是自由振動部分，在阻力下很快衰減消失；

x 2

是受迫振動部分，則

x = x 2

＝Bsin(ωt+ε) 受迫振動的振幅

B = βδ H

　　(6) 其中β為振幅放大繫數，

δ H

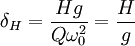為干擾力最大值作為靜荷加於彈性系統的靜位移： $\beta=\frac{1}{\sqrt{[1-(\frac{\omega}{\omega_0})^2]^2+4(\frac{n}{\omega_0})^2(\frac{\omega}{\omega_0})^2}}$ 　　(7) $\delta_H=\frac{Hg}{Q\omega_0^2}=\frac{H}{g}$ 　　(8) 於是可求得振動構件的最大動位移和最大動應力

δ d, m a x = B + δ s t,σ d, m a x = K d σ s t

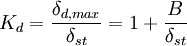　　(9) $K_d=\frac{\delta_{d,max}}{\delta_{st}}=1+\frac{B}{\delta_{st}}$ 　　(10)

[編輯]

參考文獻

↑ 金錚主編.第十五章動載荷工程力學.東南大學出版社,2010.07.
↑ 喻勛良主編.第五章材料力學工程力學.機械工業出版社,2008.3.
↑ 黃大巍,李風,毛文傑等編著.第二章輪式起重機現代起重運輸機械.化學工業出版社,2006年05月第1版.
↑ 高斌主編;李冬霞副主編.附錄Ⅲ 工程應用專題介紹工程力學.湖南大學出版社,2005年08月第1版.

取自"https://wiki.mbalib.com/zh-tw/%E5%8A%A8%E8%BD%BD%E8%8D%B7"

打开MBA智库App, 阅读完整内容打开App

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

本条目由以下用户参与贡献

连晓雾.

頁面分類: 機械 | 工業

評論(共0條)

提示:評論內容為網友針對條目"動載荷"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。

查看

工具▼

動載荷

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是動載荷^[1]

動載荷產生的原因^[2]

動載荷繫數^[3]

動載荷計算的基本方法^[4]

參考文獻

温馨提示

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

查看

工具▼

動載荷

出自 MBA智库百科(https://wiki.mbalib.com/)

目錄

什麼是動載荷[1]

動載荷產生的原因[2]

動載荷繫數[3]

動載荷計算的基本方法[4]

參考文獻

温馨提示

本條目相關文檔

本条目相关课程

本条目由以下用户参与贡献

評論(共0條)

導航

意见反馈

什麼是動載荷^[1]

動載荷產生的原因^[2]

動載荷繫數^[3]

動載荷計算的基本方法^[4]