伊藤引理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
在布朗運動方程中,我們假設參數μ和σ均為給定的常數,與wt和時間t均無關。但是某些場合,這一假設可能並不滿足。因此,布朗運動方程的一般表示形式為:
dwt = μ(wt,t)dt + σ(wt,t)dzt
我們稱上述模型為伊藤過程。對於伊藤過程來說,其瞬時期望漂移率和瞬時標準差不是常數。同樣,由於dzt服從正態分佈,則dwt也服從正態分佈。而且,
E(dwt) = μ(wt,t)dt;var(dwt) = σ2(wt,t)dt (1)
伊藤引理是日本數學家伊藤在1951年提出來的,它揭示了這樣一個規律,即一個伊藤過程的函數仍然是一個伊藤過程。
如果F(wt,t)是wt和t的一個函數,則F(wt,t)的微分dF應滿足下列隨機微分方程:
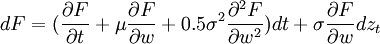 (2)
(2)
式中為了方便起見,各變數忽略了下標t,且μ = μ(wt,t),σ = σ(wt,t)比較一下(1)和(2)式不難看出,F(wt,t)仍然是一個伊藤過程,其瞬時期望漂移率為
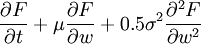
而瞬時標準差為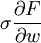
下麵簡單證明伊藤引理:
對F(wt,t)關於wt和t進行泰勒展開,並略去二階以及二階以上項,得到
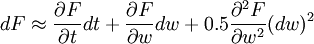 (3)
(3)
註意到,由於w是一個伊藤過程,可以由(1)式表示,另外按照證明E((dzt)2) = dt,var((dzt)2) = 0(var((dzt)2) = 0表示雖然維納過程是一個隨機過程,dzt本身是不可預測的,但是其平方卻完全可以預測。這就是說(dzt)2 = dt)式的同樣過程,可以證明
E((dw)2) = σ2dt,var((dw)2) = 0
即有
(dw)2 = σ2dt (4)
將(1)和(4)式代入(3)式即可得到伊藤引理的結論(2)式。
如果我們知道x遵循的隨機過程,通過伊藤引理可以推導出G(x,t)遵循的隨機過程。由於衍生產品價格是標的資產價格和時間的函數,因此隨機過程在衍生產品分析中扮演重要的角色。
證券價格遵循普通布朗運動,衍生證券價格和標的資產價格之間存在函數關係,數學家伊藤證明瞭衍生證券價格的隨機過程可以由標的資產的價格的隨機過程推導出。另外,伊藤引理在期權定價理論中起著十分重要的作用。 Black-Scholes正式利用該引理推導出B-S方程的,而後者又是導出期權定價模型的基礎。








(3)式寫錯了……