方差
出自 MBA智库百科(https://wiki.mbalib.com/)
方差(Variance)
目录 |
方差是各个数据与其算术平均数的离差平方和的平均数，通常以σ2表示。方差的计量单位和量纲不便于从经济意义上进行解释，所以实际统计工作中多用方差的算术平方根——标准差来测度统计数据的差异程度。
标准差又称均方差，一般用σ表示。方差和标准差的计算也分为简单平均法和加权平均法，另外，对于总体数据和样本数据，公式略有不同。
设总体方差为σ2，对于未经分组整理的原始数据，方差的计算公式为：
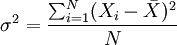
对于分组数据，方差的计算公式为：
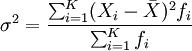
方差的平方根即为标准差，其相应的计算公式为：
未分组数据：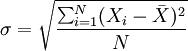
分组数据：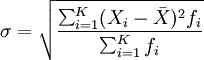
样本方差与总体方差在计算上的区别是：总体方差是用数据个数或总频数去除离差平方和，而样本方差则是用样本数据个数或总频数减1去除离差平方和，其中样本数据个数减1即n－1称为自由度。设样本方差为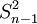
，根据未分组数据和分组数据计算样本方差的公式分别为：
未分组数据：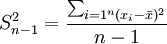
分组数据：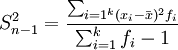
未分组数据：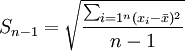
分组数据：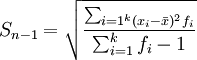
例:考察一台机器的生产能力，利用抽样程序来检验生产出来的产品质量，假设搜集的数据如下：
| 3.43 | 3.45 | 3.43 | 3.48 | 3.52 | 3.50 | 3.39 |
| 3.48 | 3.41 | 3.38 | 3.49 | 3.45 | 3.51 | 3.50 |
根据该行业通用法则：如果一个样本中的14个数据项的方差大于0.005，则该机器必须关闭待修。问此时的机器是否必须关闭？
解：根据已知数据，计算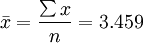
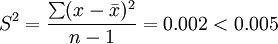
因此，该机器工作正常。
方差和标准差也是根据全部数据计算的，它反映了每个数据与其均值相比平均相差的数值，因此它能准确地反映出数据的离散程度。方差和标准差是实际中应用最广泛的离散程度测度值。
评论(共36条)
一个房间的风速与温度，测量一组数据，那这是属于样本方差还是总体方差
显然是样本方差
一个房间的风速与温度，测量一组数据，那这是属于样本方差还是总体方差
“一个”说明是整体 而且一个房间里面的空间的风速与温度都可能是不一样的 故寡人认为测的是总体方差 是相对于这一个房间“总体"而言的
有的说是除以N，有的又说是N-1。为什么？
除以N是应用于全部的数据，而除以N-1是应用于样本。
为什么总体方差与样本方差的自由度要相差1，假如把样本看作是一个总体的话，那么自由度岂不是要变会n？好像有点矛盾~~~
样本均值X=(X1+X2+....+Xn)/n 样本方差Sx=((X1-X)平方+（X2-X)平方+.....+(Xn-X)平方)/n 以上两个不等式可以消去Xn，所以未知数只有N-1个，所以除以n-1.
∑i代表什么？？？？？？
分组数据中i是第i组的意思，fi表示第i组的数据的个数 ∑i=1 k（xi-x拔）fi xi是组中值，乘以fi 是因为每组i个数据，相当于把每组的数据看成一样的，由组中值xi来表示，每组有i个数据， 同样分数线下面的 ∑i=1 k fi 是数据的总的个数
分组数据中i是第i组的意思，fi表示第i组的数据的个数 ∑i=1 k（xi-x拔）fi xi是组中值，乘以fi 是因为每组i个数据，相当于把每组的数据看成一样的，由组中值xi来表示，每组有i个数据， 同样分数线下面的 ∑i=1 k fi 是数据的总的个数
k是组数 共有k组 所以i的取值为 1 到 k
一个房间的风速与温度，测量一组数据，那这是属于样本方差还是总体方差
这组数据是一个样本，即一组数据。应该是样本方差
“样本均值X=(X1+X2+....+Xn)/n 样本方差Sx=((X1-X)平方+（X2-X)平方+.....+(Xn-X)平方)/n 以上两个不等式可以消去Xn，所以未知数只有N-1个，所以除以n-1.”
这个不太理解，有一说是自由度。都不甚明白。。
样本方差是由样本数量n来决定，为了使样本方差估计的无偏性，一旦样本均值算出，样本的决定条件就变成了n-1，所以是除以n-1。
这些都是统计学中的基本概念啊，一般来说，商科学生大一的时候就学过了。
就你知道的多
很好~谢谢~