有效久期

出自 MBA智库百科(https://wiki.mbalib.com/)

有效久期(Effective Duration)

　　有效久期是指在利率水平发生特定变化的情况下债券价格变动的百分比。它直接运用不同收益率变动为基础的债券价格进行计算，这些价格反映了隐含期权价值的变动。

　　弗兰克•法波齐(Frank Fabozzi)描述了另一种衡量久期的方法，它是从修正久期的含义发展而来的。有效久期是衡量不同利率水平下债券价格敏感性的方法。在收益率发生很小变动时它是修正久期的近似值。有效久期对可赎回债券或其他期限和现金流不确定的证券尤为有用。

　　在Macaulay久期模型研究中存在一个重要假设，即随着利率的波动，债券的现金流不会发生变化。然而这一假设对于具有隐含期权的金融工具，如按揭贷款、可赎回(或可卖出)债券等而言则很难成立。因此，Macaulay久期模型不应被用来衡量现金流易受到利率变动影响的金融工具的利率风险。针对Macaulay久期模型这一局限，FrankFabozzi提出了有效久期的思想。所谓有效久期是指在利率水平发生特定变化的情况下债券价格变动的百分比。它直接运用不同收益率变动为基础的债券价格进行计算，这些价格反映了隐含期权价值的变动。

　　有效久期不需要考虑各期现金流的变化情况，不包含利率变化导致现金流发生变化的具体时间，而只考虑利率一定变化下的价格总体情况。因此，有效久期能够较准确地衡量具有隐含期权性质的金融工具的利率风险。对于没有隐含期权的金融工具，有效久期与修正久期是相等的。

　　随着对久期模型研究的不断深入，相继有人提出了方向久期、偏久期、关键利率久期、近似久期以及风险调整久期等新的久期模型，把利率的期限结构、票息率的改变以及信用风险、赎回条款等加入到模型里面，使久期模型得到了进一步的发展。

　　用下列公式可以计算有效久期：

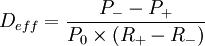
　　其中：

• P_——利率下降x个基本点时的债券价格；
• P+——利率上升x个基本点时的债券价格；
• R_——初始收益率减去x个基本点；
• R+——初始收益率加上x个基本点；
• P0——债券的初始价格。

　　例：考虑8年期利率为9.5％的债券，半年支付1次利息，按面值90％出售，其到期收益率为11.44％。我们现在用收益率中5个基本点的变化来计算其有效持续期。收益率为11.49％时，相关债券价格为89.77％元，收益率11.39％时，价格为90.25％。

• 修正持久期
• 麦考利久期