马科维茨的均值一方差组合模型
出自 MBA智库百科(https://wiki.mbalib.com/)
马科维茨的均值一方差组合模型(Markowitz Mean-Variance Model,Markowitz Model简称MM)
目录 |
证券及其它风险资产的投资首先需要解决的是两个核心问题:即预期收益与风险。 那么如何测定组合投资的风险与收益和如何平衡这两项指标进行资产分配是市场投资者迫切需要解决的问题。正是在这样的背景下,在50年代和60年代初,马可维兹理论应运而生。
该理论依据以下几个假设:
1、投资者在考虑每一次投资选择时,其依据是某一持仓时间内的证券收益的概率分布。
2、投资者是根据证券的期望收益率估测证券组合的风险。
3、投资者的决定仅仅是依据证券的风险和收益。
4、在一定的风险水平上,投资者期望收益最大;相对应的是在一定的收益水平上,投资者希望风险最小。
根据以上假设,马可维兹确立了证券组合预期收益、风险的计算方法和有效边界理论,建立了资产优化配置的均值-方差模型:
目标函数:minб2(rp)=∑ ∑xixjCov(ri,rj)
rp= ∑ xiri
限制条件: 1=∑Xi (允许卖空)
或 1=∑Xi xi>≥0(不允许卖空)
其中rp为组合收益, ri为第i只股票的收益,xi、 xj为证券 i、j的投资比例,б2(rp)为组合投资方差(组合总风险),Cov (ri 、rj ) 为两个证券之间的协方差。该模型为现代证券投资理论奠定了基础。上式表明,在限制条件下求解Xi 证券收益率使组合风险б2(rp )最小,可通过朗格朗日目标函数求得。其经济学意义是,投资者可预先确定一个期望收益,通过上式可确定投资者在每个投资项目(如股票)上的投资比例(项目资金分配),使其总投资风险最小。不同的期望收益就有不同的最小方差组合,这就构成了最小方差集合。
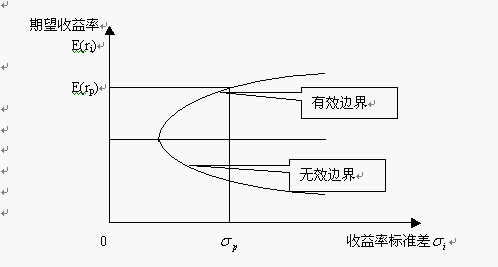
马科维茨的投资组合理论不仅揭示了组合资产风险的决定因素,而且更为重要的是还揭示了“资产的期望收益由其自身的风险的大小来决定”这一重要结论,即资产价格(单个资产和组合资产)由其风险大小来定价,单个资产价格由其方差或标准差来决定,组合资产价格由其协方差来决定。马可维茨的风险定价思想在他创建的“均值-方差”或“均值-标准差”二维空间中投资机会集的有效边界上表现得最清楚。下文在“均值-标准差”二维空间中给出投资机会集的有效边界,图形如下:
上面的有效边界图形揭示出:单个资产或组合资产的期望收益率由风险测度指标标准差来决定;风险越大收益率越高,风险越小收益率越低;风险对收益的决定是非线性(二次)的双曲线(或抛物线)形式,这一结论是基于投资者为风险规避型这一假定而得出的。具体的风险定价模型为:
其中![]() ,且A,B,C,D为常量;R表示N个证券收益率的均值(期望)列向量,Ω为资产组合协方差矩阵,1表示分量为1的N维列向量,上标T表示向量(矩阵)转置(公式(5)的推导过程。
,且A,B,C,D为常量;R表示N个证券收益率的均值(期望)列向量,Ω为资产组合协方差矩阵,1表示分量为1的N维列向量,上标T表示向量(矩阵)转置(公式(5)的推导过程。
马可维茨的风险定价思想和模型具有开创意义,奠定了现代金融学、投资学乃至财务管理学的理论基础。不过这种理论也有缺点,就是他的数学模型较为复杂,不便于实际操作。








本栏目办得好