预测波动率

出自 MBA智库百科(https://wiki.mbalib.com/)

　　预测波动率又称为预期波动率，它是指运用统计推断方法对实际波动率进行预测得到的结果，并将其用于期权定价模型，确定出期权的理论价值。因此，预测波动率是人们对期权进行理论定价时实际使用的波动率。这就是说，在讨论期权定价问题时所用的波动率一般均是指预测波动率。需要说明的是，预测波动率并不等于历史波动率，因为前者是人们对实际波动率的理解和认识，当然，历史波动率往往是这种理论和认识的基础。除此之外，人们对实际波动率的预测还可能来自经验判断等其他方面。

　　（一）移动平均法

　　移动平均法是指以过去N天的收益率的方差作为当日波动率的估计值，分为简单移动平均和加权移动平均两种方法。简单移动平均法将每天的收益率看成是等权重的，加权移动平均法则对不同时点赋予不同的权重。

　　简单移动平均法：

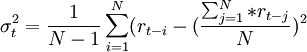
　　加权移动平均法：

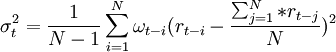
　　其中，r_{t − i}为t-i时刻的收益率，ω_{t − i}为t-i时刻的权重。

　　（二）指数平滑法

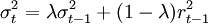
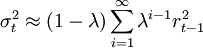
　　其中，λ为衰退因子，即平滑系数，0<λ<1。

　　将指数平滑公式通过递推推导，可以得到t时刻的波动率σ与收益率r之间的关系式。运用此方法，需要确定参数λ。

　　（三）GARCH模型法

　　借助Garch模型，可以估计和预测波动率。

　　Bollerslev于1986年对自回归条件异方差模型（ARCH）进行了推广，提出了广义自回归条件异方差模型（GARCH）。标准的Garch(q,p)模型为：

　　y_t = X_tΥ + μ

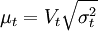
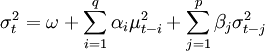
　　其中，p是GARCH项的次数，q是ARCH项的次数,σ是条件方差。

　　此外，还有随机波动模型（SV）以及其扩展模型、自回归移动平均模型（ARIMA/ARFIMA）等，用于对金融资产波动率的估计。另外，也可以通过模型预计隐含波动率。