遍历理论

出自 MBA智库百科(https://wiki.mbalib.com/)

遍历理论(Ergodic Theory)

　　遍历理论是研究保测变换的渐近性态的数学分支。它起源于为统计力学提供基础的“遍历假设”研究，并与动力系统理论、概率论、信息论、泛函分析、数论等数学分支有着密切的联系。

　　在统计学中，遍历理论是指在统计力学发展的中期，冯·诺伊曼(Von Neumann)和伯克霍夫(Birkhoff)给出了识别具有时间平均的空间平均问题的解答。可以表述如下:如果x₁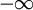（<t<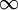）表示一个保守的动态系统轨道，在时间t = 0时，通过点r = r₀，在此系统的相空间Ω上定义的适当函数：

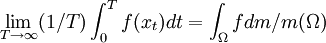
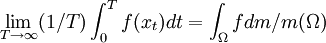　　方程式的左边是一个沿着轨道对于函数(可观察的)f的时间平均，而右边是相或空间平均。

　　冯·诺伊曼证明了该式的一个平均收敛形式，以后不久，G·D·伯克霍夫证明了该式，正如他所说的，对于几乎所有的状态，包括这里的两种情况，都是在假设系统(限于Ω)为遍历的情况下得到的。遍历是一种概念，我们现在来解释它(冯·诺伊曼，1932年;伯克霍夫，1931年)。人们很快就认识到，(遍历定理)的两种形式可以在更加抽象的背景下描述和证明。诚然，人们可以说，这种抽象和由此而产生的数学式子就是遍历理论本身。

　　令(Ω,m)代表一个有限维的抽象空间，(假设m(Ω) = 1也不失一般性，正如我们将要做的。)设T_t为一个变换族，下标是时间(在各种情况下，它是一个实数、整数)。假设这一族变换是保测变换(mT_tB = mB，对于所有的“可测”集均成立)。那么，当才在它的指标集中变化时对T_t的研究，就提供了一个渐近系统模型，这样的渐近系统如同前面描述的相空间中的动态学系统一样，在其中的测度(体积)是被保证的。如果O不能被分解成两个不相交的不变可测集A,B(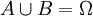,,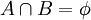 T_tA = A_t,T_tB = B)所有t那么就称上述这样的系统是遍历系统。

　　在严格的意义上来说，时间平均空间平均问题并不是由冯·诺伊曼和伯克霍夫解决的，远在开始产生古典的动态系统的时候就已经涉及到，但对这样的系统是否是遍历系统的问题并未解决。

　　在遍历理论方面，大部分研究者所关心的是用整数作下标的保测变换T_t本身的问题，也就是T_t = T,T_t是T的t次迭代。在这方面的结果必然导致实连续时间的结果。

　　继伯克霍夫和冯·诺伊曼的开创性工作之后，许多数学家对个体及平均遍历定理作了种种推广。它包括：把平均遍历定理推广到更一般的巴拿赫空间和更一般的变换；把关于点变换的平均遍历定理推广到关于马尔可夫过程的平均遍历定理；把关于离散半群φk的个体及平均遍历定理推广到更一般的单参数半群φt甚至多参数的情形，等等。由许多数学研究者得到的遍历定理的各种提法有：极大遍历定理，一致遍历定理，受控遍历定理，局部遍历定理，阿贝尔遍历定理和次可加遍历定理等等。保测变换的谱理论研究，则是遍历理论与泛函分析相关联的重要课题。

　　上面提到的遍历理论的研究工作，都假定事先有了一定的测度。在数学研究中还可以提这样一类问题：给定拓扑空间Χ上的连续变换φ，是否存在Χ上的概率测度μ使其成为保测变换？这样的测度是否唯一？这又引起了关于不变测度的研究。数学上已经证明：对于紧致的可度量化的空间Χ的连续变换φ，不变测度必定存在。如果这种不变测度μ是唯一的，那么φ关于该测度就必定是遍历的，这时称变换φ具有唯一遍历性。

　　1958年Α.Η.柯尔莫哥洛夫在保测变换的研究中引进了测度熵的概念。测度熵反映了变换紊乱的程度，其物理背景正是热力学中的熵。测度熵的引进是继伯克霍夫和冯·诺伊曼工作之后保测变换研究中的又一重大进展。测度熵作为不变量为研究保测变换的同构问题提供了重要的工具。这一工具最初的效果是辨明了一些过去长期无法区分的系统的不同构。1970年D.奥恩斯坦获得了正面肯定同构的重要成果，他证明了具有相同测度熵的伯努利移位是同构的。类比于测度熵，R.L.阿德勒、A.G.康海姆和M.H.麦克安德鲁等人1965年在动力系统理论的研究中引入了拓扑熵的概念。