逆向归纳法
出自 MBA智库百科(https://wiki.mbalib.com/)
逆向归纳法(backward induction)是求解动态博弈均衡的方法
目录 |
逆向归纳法(backward induction)是求解动态博弈均衡的方法。所谓动态博弈是指博弈参与人的行动存在着先后次序,并且后行动的参与人能够观察到前面的行动。逆向归纳法在逻辑上是严密的,然而它存在着“困境”。所谓逆向归纳法是从动态博弈的最后一步往回推,以求解动态博弈的均衡结果。逆向归纳法又称逆推法。它是完全归纳推理,其推理是演绎的,即结论是必然的。[1]
在完全且完美的动态博弈中,先行为的理性博弈人,在前面阶段选择策略时,必然会考虑后行博弈人在后面阶段中将会怎样选择策略。因而,只有在博弈的最后一个阶段,不再有后续阶段牵制的情况下,博弈人才能作出明智的选择。在后面阶段博弈人选择的策略确定后,前一阶段的博弈人在选择策略时也就相对容易。
逆向归纳法就是从动态博弈的最后一个阶段开始分析,逐步向前归纳出各阶段博弈人的选择策略。
逆向归纳法的逻辑基础:动态博弈中先行动的参与人,在前面阶段选择行为时必然会考虑后行动的参与人在后面阶段中的行为选择,只有在最后一阶段的参与人才能不受其他参与人的制约而直接做出选择。而当后面阶段的参与人的选择确定后,前一阶段的参与人的行为也就容易确定了。逆向归纳法排除了不可信的威胁或承诺。
逆向归纳法:它的精髓就是“向前展望,向后推理”,即首先仔细思考自己的决策可能引起的所有后续反应,以及后续反应的后续反应,直至博弈结束;然后从最后一步开始,逐步倒推,以此找出自己在每一步的最优选择。[1]
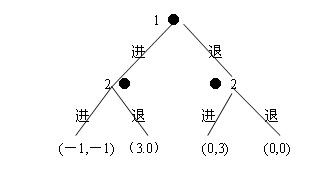
图1的求解过程如下:
- (a)若2在右,2将选择进(0.3);∵(0.3)>(0.0)
- (b)若2在左,2将选择退(3.0);∵(3.0)>(-1.-1)
- (c)在2的选择中1的最大收益是选择进;∵(3.0)>(0.3)
- ∴纳什均衡为(进(进,退))均衡解为(进,退),均衡收益为(3.0)
(2)逆向归纳法仅适合有限步动态博弈,而且要求决策者犯的可能性很小。
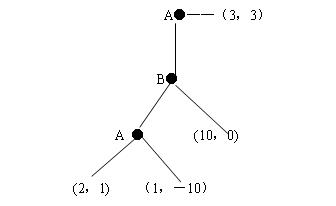
如果使用逆向归纳法得到的结果是A选择右边的行动,双方各得3。
如果A在第一步选择下边的行动,B该做何想?只有当A在第二步犯错误的可能性小于1/11时,B才有胆量选择让游戏继续玩下去。于是A极有可能获得10这个最大回报。
对逆向归纳法的批评[2]
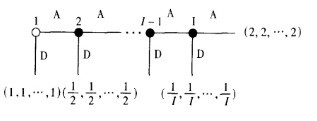
右图所描述的I个参与人的博弈,在这里,每一个参与人i<I可以选择“D”来结束博弈,或者选择“A”把采取行动的权利让给参与人i+I。如果参与人i选择了行动D,每一个参与人都能得到l/i;如果所有参与人都选择了行动A,那么每一个参与人都能得到2。
由于每次只有一个参与人采取行动,这是一个完美信息博弈,我们可以应用逆向归纳方法。用这一方法可以预测得每一个参与人应该都会选择行动A。如果I很小,这似乎是一个合理的预测。如果I很大,那么作为参与人1,我们自己将都会选择D而不是A,其原因类似于猎鹿博弈中推导无效率均衡所用到的“稳健性”。
首先,收益2要求所有I—1个其他参与人都要选择行动A。如果一个给定参与人选择行动A的概率是P<l,并且与其他参与人的选择是相互独立的,那么所有其他I-1个参与人都选择行动A的概率就是pI − 1,这一概率是很小的(即使p很大)。其次,我们会担心参与人2可能也会有着同样的考虑;也就是说,参与人2可能会选择D,以防未来参与人出现“失误”或者参与人3故意选择D的可能。
一个相关结论是逆向归纳的链条越长,则其所假定的前提假设的链条也就越长(“参与人1知道参与人2知道参与人3知道……的收益”)。如果在图中,I=2,逆向归纳假设参与人1知道参与人2的收益,或者至少参与人1充分地相信参与人2的最优选择是A。如果I=3,不仅参与人l和参与人2了解参与人3的收益,而且参与人1还必须知道参与人2清楚参与人3的收益,从而参与人l可以预测参与人2对参与人3的行动预测,如果参与人1认为参与人2将会不正确地预测参与人3的行动选择,那么参与人1就会选择行动D。习惯上,均衡分析是建立在收益作为一种“共同知识”的前提上的.从而任意长的“i知道j知道k知道”是有效的,但比起需要稍弱的共同知识前提假设所得列的结论,由这种形式的非常长链所得到的结论似乎更不合理(部分原因足由于逆向归纳的链条越长,就会对博弈信息结构的微小变化越敏感。)
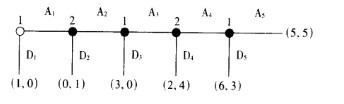
在右上图所示的例子中,如果I非常大的话,那这一博弈就变得极为麻烦了。当同—个参与人可以接连几次采取行动时,就会出现逆向归纳法中的第二个难点。考察右图所示的博弈。在这里,逆向归纳法的解就是采取行动参与人在每一个信息集上都采取行动D。这一解是否具有说服力呢?设想你就是参与人2;设想,与原来的预期相反,参与人1在他初次采取行动时选择了行动A1,你将会怎样行动呢?逆向推理法表明你应选择行动D2,因为若给予参与人l下一次机会时他将选择D3;然而,逆向归纳法也表明参与人1本应是选择D1。
在这一博弈中,参与人2在参与人l偏离了其所预测的行动选择A1时,参与人2的最优选择取决于自己如何认为参与人1在未来的行动:若参与人2认为存在至少25%的可能性参与人1会选择行动A3,则参与人2应选择行动A2。参与人2又是如何形成这些信念,并且到底什么信念才是合理的呢?尤其是,与逆向归纳法相反,如果参与人1决定选择行动A1,那么参与人2将应怎样去预测参与人1的行动?在某些文章的讨论中,选择行动A2似乎是一个有利可图的赌博。
在经济学文献中,大部分的动态博弈分析仍然是毫无保留地使用逆向归纳法及其精炼,但近来对这一点持有怀疑态度的人多了起来。在右图中所示的博弈是基于罗森泰尔(Rosenthal,1981)的例子,他是首先对逆向归纳法的逻辑性提出质疑的人之一。贝苏(Basu,1988,1998),鲍那诺(Bonanno,1988),宾默尔(Binmore,1987,]988)以及伦尼(Reny,1986)论证,合理的博弈理产不应该在理论给定为0概率的事件发生时就排除行动选择,因为理论并没有给参与人提供在这些事发生的条件下如何建立他们预测的途径。弗登博格、克瑞普斯和莱维的研究建议参与人把意外的偏离解释成由于收益与原来所认定最有可能的情况发生偏差。因为任何博弈结果都可以解释为对竞争对手收益的某种确认,这种方法就回避了再零概率事件发生时如何形成信念的困难,它把发生“偏离”后如何去预测博弈问题改变为在给定观察到的行动下哪—个另类收益是最可能的问题。弗登博格与克瑞普斯把它进一步扩展上升为一种方法论:他们论证任何博弈理论应该在某种意义上是“完备”的,即给任何可能的博弈行动赋予严格正的概率。运用这一理轮,参与人对后面博弈的条件预测总是有定义的。
收益不确定性不是建立一个完备理论的惟一方法。第二类方法是把任何扩展式博弈解释为隐含参与人有时会犯一些小“错误”或“颤抖”(如泽尔滕1975提出的)。如泽尔滕所假设的,如果在不同信息集上“颤抖”的概率是相互独立的,那么无论过去多么频繁出现与逆向归纳法预测不符的情况,参与人都应继续在当前子博弈中运用逆向归纳法来预测博弈行动,因此,把偏离用“颤抖”来解释是一种为逆向归纳法辩护的方法。与之相关的问题是,参与人在多大程度上会把这种对偏离的“颤抖”解释看做是反对其他理论解释的依据。在右图2中,如果参与人2观察到A1,那么他(或她)应该把这种情况解释为一种“颤抖”,还是看做参与人1将会选择A3种信号呢?
逆向推理法的案例分析[3]
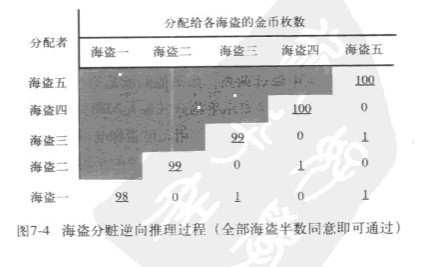
海盗分赃逆向归纳法的经典例子,其原型来自I.Stewart在《科学美国人》杂志上的一篇文章《凶残海盗的逻辑》。这个例子曾经被作为微软公司招募员工的面试题目,你也可以尝试着可以在几分钟之内求解出正确答案。
- 1.故事模型
话说有5个海盗抢来了100枚金币,大家决定分赃的方式是:由海盗一提出一种分配方案,如果同意这种方案的人达到半数,那么该提议就通过并付诸实施;若同意这种方案的人未达半数,则提议不能通过且提议人将被扔进大海喂鲨鱼,然后由接下来的海盗继续重复提议过程。假设每个海盗都绝顶聪明,也不相互合作,并且每个海盗都想尽可能多得到金币,那么,第一个提议的海盗将怎样提议既可以使得提议被通过又可以最大限度得到金币呢?
我曾好几次在学生中做过调查,如果他们就是第一个海盗会怎么分。答案五花八门,但是大多数是表示平均分(每人20颗)——这可能是现实中的情况,公平观念在博弈中发挥着作用。但是标准博弈论是研究人们完全理性的情况下极端复杂的策略互动后果,这里的平均分配并不符合标准博弈论的逻辑。
那么答案究竟是什么呢?使用逆向归纳法可以求解如下:
- 首先,考虑只剩下最后的海盗五,显然他会分给自己100枚,并赞成自己。
- 再回溯到只剩下海盗四和海盗五的决策,海盗四可以分给自己100枚并赞成自己;海盗五被分得0枚,即使反对也无用。
- 回到海盗三,海盗三可以分给海盗五l枚得到海盗五的同意;分给自己99枚,自己也同意;分给海盗四0枚,海盗四反对但无用。
- 回到海盗二,海盗二可以分给海盗四1枚得到海盗四同意;分给自己99枚,自己也同意;海盗三、五各分得0枚,他们会反对但反对没有用。
- 回到海盗一,他可以分给海盗三、五各l枚,获得海盗三、五的同意;分给自己98,自己也同意;分给海盗二、四各0枚,他们会反对但反对不起作用。
因此,这个海盗分赃问题的答案是(98,0,1,0,1):海盗一提出分给自己98枚,分给海盗二、四各0枚,分给三、五各1枚,该提议会被通过,因为海盗一、三、五会投赞成票。我们可以把这个逆向决策的过程用如下矩阵表达出来(如上图,其中画下划线的数字表示海盗对该方案投了赞成票,未加下划线对应于反对票)。
如果你是海盗一,你会这样提方案吗?
对于上述海盗分赃问题,我们还可以演化出不同的版本。比如说:(1)如果要求包括提议海盗在内的所有海盗过半数(超过1/2)同意才能使提议通过,那么海盗一应该怎么提方案?(2)如果要求提议海盗之外的海盗过半数同意才能通过,那么海盗一又该怎么提方案?(3)或者海盗的数目增加到10个、100个,海盗一又怎么提方案?大家可以把这个当做练习题来做一做。
答案:变种问题(1)中,海盗一一提出的分配方案是(97,0,1,2,0)或(97,0,1,0,2);变种问题(2)中,海盗一提出的分配方案应是(97,0,1,1,1);变种问题(3)中,大家可尝试逐渐增加海盗的数量,将会发现答案是有规律可循的。
评论(共18条)
实话实说,一点都没看懂!!
倒推,也就是逆向思维。你若选1那下一个会选什么呢。选2呢?。然后再回头选最有利的那一方案
图1 的求解过程 (a) 里是不是有错误??
应该是(0.3)>(0.0)
恩恩,我也看出来了
第二个图 为啥是1/11呢
你好,因为如果处在第二阶段的B给A第二次做选择的机会,那么理性的B必须保证即将进行的第三阶段博弈(A第二次选择)出现,其收益要大于第二阶段博弈(B选择r(10,0)) 所以设A选择LEFT的概念为(1-P),那么A犯错的概率选择RIGHT为P,所以第三阶段B的收益为1-P+(-10)P要大于等于第二阶段的0,解出来就是P《1\11.
兔宝宝我爱你——猪猪
一个口袋里面有100个球,有5个人依次去取球,球的数量可以自己决定。当取球结束时,手里拿球最多的和最少的都要死去。现在问你1~5个人哪个位置最容易存活?怎么取球?
一个口袋里面有100个球,有5个人依次去取球,球的数量可以自己决定。当取球结束时,手里拿球最多的和最少的都要死去。现在问你1~5个人哪个位置最容易存活?怎么取球?
這裡有一個關鍵問題是,袋子裡的100顆球一定要拿完嗎?
实话实说,一点都没看懂!!
For real? It is so damn easy to understand.
我的疑问,问什么海盗一分给别人1枚,别人就同意他?!不可想象,最起码100枚应该在海盗一选的几个人里面平分吧?
海盗是极其聪明的,如果不同意,那么他的收益肯定比1还低。
为啥 海盗 分得 1枚金币,就会同意呢?
对呀,第一个海盗敢这么分就被扔下去了
对呀,第一个海盗敢这么分就被扔下去了
要么1要么0,大概是这意思吧~








实话实说,一点都没看懂!!