迪尼定理
出自 MBA智库百科(https://wiki.mbalib.com/)
迪尼定理(Dini's theorem)
目录 |
在数学中,迪尼定理叙述如下:设 X 是一个紧致的拓扑空间, f(n) 是 X 上的一个单调递增的连续实值函数列(即使得对任意 n 和 X 中的任意 x 都有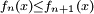 )。如果这个函数列逐点收敛到一个连续的函数 f ,那么这个函数列一致收敛到 f 。这个定理以意大利数学家乌利塞•迪尼命名。
)。如果这个函数列逐点收敛到一个连续的函数 f ,那么这个函数列一致收敛到 f 。这个定理以意大利数学家乌利塞•迪尼命名。
对于单调递减的函数列,定理同样成立。这个定理是少数的由逐点收敛可推出一致收敛的例子之一,原因是由单调性这个更强的条件。
注意定理中的 f 一定要是连续的,否则可以构造反例。比如说在区间 [0,1] 上的函数列 {xn}。这是一个单调递减函数,逐点收敛到函数 f :当 x 属于 [0,1) 时f(x) 等于 0 ,f(1) 等于 1。但这个函数列不是一致收敛的,因为 f 不连续。
我们对单调递增的函数列作证明:对于任意 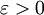 ,对每个 n ,设
,对每个 n ,设 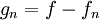 再设
再设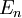 为使得
为使得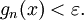 的
的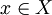 。显然每个gn 都连续,于是每个En 都是开集(在拓扑空间中,连续函数被定义为使得开集的原像都是开集的函数,可以证明这种定义和一般的连续定义是等价的,而
。显然每个gn 都连续,于是每个En 都是开集(在拓扑空间中,连续函数被定义为使得开集的原像都是开集的函数,可以证明这种定义和一般的连续定义是等价的,而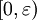 是正实数集中的开集)。函数列{gn} 是单调递减的,因此En 是En + 1 的子集。又由于
是正实数集中的开集)。函数列{gn} 是单调递减的,因此En 是En + 1 的子集。又由于 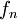 逐点收敛到 f ,所有(En) 的并集是 X 的一个开覆盖。但是 X 是一个紧集于是存在正整数 N 使得EN = X。因此对所有 n > N,对所有的
逐点收敛到 f ,所有(En) 的并集是 X 的一个开覆盖。但是 X 是一个紧集于是存在正整数 N 使得EN = X。因此对所有 n > N,对所有的 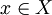 ,都有
,都有 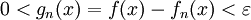 ,于是{fn} 一致收敛于 f 。
,于是{fn} 一致收敛于 f 。







