贝叶斯决策法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　决策的分类有很多种，如果按环境划分，决策可以分为确定型、不确定型和风险型三大类，其中风险型决策是最常见的类型。风险型决策的主要特点是具有状态发生 的不确定性。决策者面临着几种可能的状态和相应的后果，且对这些状态和后果得不到充分可靠的有关未来环境的信息，只能依据“过去的信息或经验”去预测每种状态和后果可能出现的概率，在这种情况下，决策者根据确定的决策函数计算出项目在不同状态下的函数值，然后再结合概率求出相应的期望值，此值就是对未来可能出现的平均状况的估计，决策者可以依此期望值的大小做出决策行为。常见的决策函数主要有成本函数、收益函数、效用函数。前面两种函数是从货币因素考虑的，而后者是从非货币因素考虑的。这种以期望值为标准的分析法是决策者在处理风险型问题时常常使用的方法，贝叶斯决策法是最常见的以期望为标准的分析方法。它是在不完全情报下，对部分未知的状态用主观概率估计，然后用贝叶斯公式对发生概率进行修正，最后再利用期望值和修正概率做出最优决策。

　　如果决策函数是成本函数或收益函数，则决策者是从货币因素考虑问题的。贝叶斯决策模型是决策者在考虑成本或收益等经济指标时经常使用的方法，它是在贝叶斯定理的基础上提出来的。以收益型问题为例，其基本思想是在已知不确定性状态变量θ的概率密度函数f(θ)的情况下，按照收益的期望值大小,对决策方案排序，则最优方案为使期望收益最大的方案。由于由贝叶斯定理可以推出通过抽样增加信息量能够使概率更加准确，概率准确则意味着决策风险的降低，所以贝叶斯定理保证了该决策模型的科学性。

　　1．收益函数的贝叶斯决策步骤

　　(1)计算出每种状态的概率，计为P_i。

　　(2)对于收益型问题，列出条件收益的计算公式，求出在各种状态下相应方案的条件收益CP_ij，结合概率求出相应的期望值EP_ij列出贝叶斯决策法收益表。

　　(3)通过贝叶斯决策法收益表，依次求出在各种状态下可获得的最大期望收益值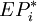，它们的和为该问题最理想的期望收益EPC，此时收益最大。

　　(4)通过贝叶斯决策法收益表，求出各方案下的期望收益EMV，其中最大的值记为EMV ^* ，使期望收益最大的方案就是最优方案。ECC与EMV ^* 的差值表示完全情报价值，计为EVPI。

　　(5)写出答案：最优方案a ^* =? EMV ^* =? EVPI=?

　　2．收益函数的贝叶斯决策模型举例

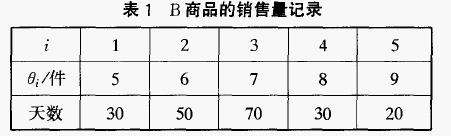
　　表1为某百货商场过去200天关于商品B的日销售量纪录，商品B的进价为200元／f牛，售价为600元／f牛，如果当天销售不完，余下全部报废，求该商品的最佳日订货量a ^* ，及相应的期望收益金额EMV ^* 和EVPI。

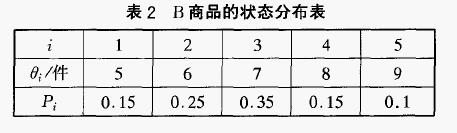
　　由表1可知，该商场商品B的销售状态空间为θ={θ₁，θ₁，θ₁，θ₁，θ₁}={5，6，7，8，9}，这些状态发生的概率也可以推测出来，见表2。根据此状态空间，决策者的决策空间为A={a₁，a₁，a₁，a₁，a₁}={5，6，7，8，9}。

　　当商场的销售量为θ_i，而进货量为a_i时，商场的条件收益为：

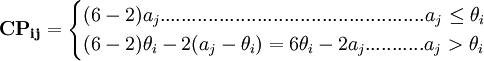
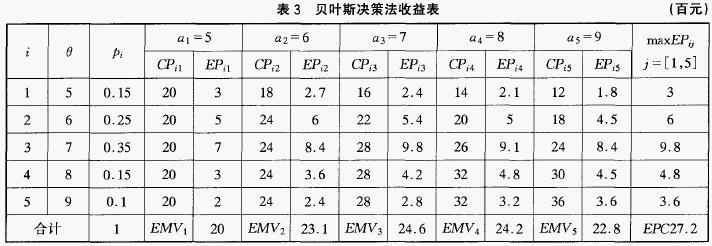
　　而相应的期望收益为EP_ij = CP_ij * P_I，表3即为此例的贝叶斯决策法收益表：

　　从经济角度看当日订货量等于日销售量时，商场没有因为多定货或少定货而造成的机会损失，因此获得的收益最大，所以此例理论上的最大利润为EPC=2,720元。但在实际工作中这个值很难得到，除非商场能够根据情况随时调整进货量，因此商场的经营者往往追求的是期望收益的最大值，在此例中当订货量为7时期望收益最大，EMV ^* 和EVP，分别为2,460元和260元。

　　EVPI的含义为由于情报不准确而造成的商场的赢利损失，这个损失可能是因为销售量小于7件而引发商品报废产生的损失，也可能是因为销售量大于7件使商场未能多盈利而造成的损失。商场若有百分之百准确的情报，则完全可以避免这类损失，因此定义EVPI为完全情报价值。

　　为了追求更多的利润，决策者总是希望获取一些准确信高的信息，现在随着越来越多的咨询公司、研究中心的出现，为我们获取高质量的信息提供了可能。只要费用小于预期收入，决策者就可以考虑购买由信息公司提供的情报信息。这些信息主要是通过抽样调查或其他途径得到的概率，与凭借经验预测出来的概率不同它们的可靠性更高，这种概率称为后验概率，而前者称为先验概率。一般的用后验概率代替先验概率进行贝叶斯决策，往往可以得到更准确的方案，这种用后验概率代替先验概率再进行贝叶斯决策，就成为后验分析法。需要指出的是有些情况下并非用后验分析法就一定比先验分析好，如果两者选择的方案相同，则意味着后者在增加成本的情况下收益并没有增加，显然此时先验比后验更加有效率。

　　决策者在进行决策时可以从货币因素出发进行决策，但因为决策的结果是由决策者承担的，所以决策者个人的心理因素就会对决策的过程产生一定的影响。在众 多心理因素中决策者对待风险的态度往往是决定性的因素。同样的问题对于风险稳重者，为了少承担风险，往往少订商品以避免商品的积压；而对于风险爱好者，他对未来的预期很高，则会冒险订购较多的商品；而对待风险持中间型态度的决策者则往往只单纯的从货币因素进行考虑。由于对风险的态度不同，所以不同的订货量给决策者所带来的满意程度也是不同的，而效用函数则可以表示这种不同。决策者会选取效用最大的方案作为候选方案。

　　1．效用函数决策步骤

　　(1)计算出每种状态的概率，计为P_i。

　　(2)列出效用函数，求出在各种状态下相应方案的效用值U(θ_i,a_i)，结合概率求出相应的期望值EU_ij，列出效用决策表。

　　(3)通过效用决策表，求出各方案下的期望效用EU_i，其中最大的记为EU _* ，使期望效用最大的方案就是最优方案。

　　(4)写出答案：最优方案a ^* =?; EU ^* =?。

　　2．效用函数决策模型举例

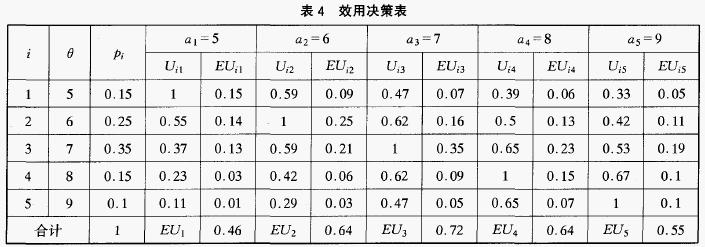
　　仍然讨论上面的例子，假设决策者为风险稳重者，其效用值随着日定货量和日销售量的差值的增大而减小，且当日定货量等于日销售量时，决策者最满意，此时效用值为1，故假设效用函数为下式，据此可构建效用决策表(见表4)。

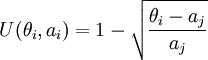
　　由表4可知，决策者的效用随着定货量与其加权平均和(6,8)的差距的加大而呈递减趋势，当定货量是7时，决策者获得最大的效用，即EU ^* = 0.72。可见此时的决策者属于风险稳重者，需要说明的是最优方案的选取是与决策者当时所采用的效用函数有紧密联系的。

　　在上面讨论的两种方法中，都是按期望值的大小进行决策的。然而对于不同的方案，即使期望值相同，它们取值的离散程度仍然是不同的，显然期望值大而离散程度小的方案是最优方案。为了考虑在单位期望值下不同方案的波动性的大小，决策者可以通过计算不同方案的变异系数υ:

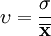
　　σ是标准差，而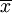是期望值。在单位期望值下，变异系数值小表示变量值密集，反之则表示变量值分散。

　　在上面的例子中，如果选择第二种方法中的效用函数作为决策函数，则相应的变异系数可以计算出来，分别为：0.578，0.347，0.278，0.195，0.282。其结果说明，在单位期望效用值下，方案a₄的波动性最小。尽管方案a₃的效用值较大，但是如果决策者从波动性的角度考虑，最优方案则应该是a₄。

　　由于在生活当中许多自然现象和生产问题都是难以完全准确预测的，因此决策者在采取相应的决策时总会带有一定的风险。贝叶斯决策法就是将各因素发生某种变动引起结果变动的概率凭统计资料或凭经验主观地假设，然后进一步对期望值进行分析，由于此概率并不能证实其客观性，故往往是主观的和人为的概率，本身带有一定的风险性和不肯定性。

　　虽然用期望的大小进行判断有一些风险，但仍可以认为贝叶斯决策是一种兼科学性和实效性于一身的比较完善的用于解决风险型决策问题的方法，在实际中能够广泛应用于组织系统改革、企业效益、市场开发、证券投资等诸多领域。使用时根据决策者的侧重点，结合变异系数，综合使用货币因素的贝叶斯决策、或效用函数的贝叶斯决策法，都会得到自己想要的结果。