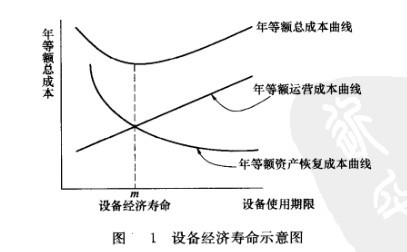
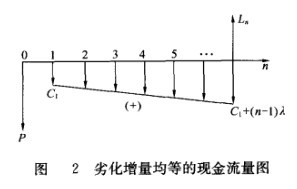
设备经济寿命

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什么是设备经济寿命

　　设备经济寿命是指设备从开始使用到继续使用直至在经济上不合理为止的整个时间周期。设备在使用过程中，由于有形磨损日益严重而使各项费用逐渐增加，可能造成继续使用的成本超过购买新设备来使用的成本；或是由于市场售价较低、性能更完善、生产效率更高的新设备出现，使得原有设备继续使用在经济上不合算。这样一来，即使设备还能用下去，从经济上考虑也面临着是否更换的选择，从而提出了经济寿命的概念。因此，设备的经济寿命是由其有形磨损和无形磨损综合作用形成的，经济寿命的长短主要取决于设备使用过程中的经济状况(费用和收益状况)。^[1]

[编辑]

设备经济寿命的确定^[2]

　　在设备更新分析中，往往要根据设备的经济寿命确定设备的更新时机，因而采用科学合理的方法来计算设备的经济寿命显得十分重要。在以下分析中我们假设设备产生的收益是相同的，只比较设备的成本。

　　1．经济寿命的静态计算方法

　　在利率为零的条件下，设备年等额总成本的计算公式如下：

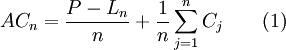
　　 $AC_n=\frac{P-L_n}{n}+\frac{1}{n}\sum_{j=1}^n C_j \qquad (1)$

　　式中

　　n——设备使用期限，在设备经济寿命计算中，n是一个自变量；

　　j——设备使用年度，j的取值范围为1到n；

　　 $A C n$ ——n年内设备的年等额总成本；

　　P——设备的购置成本，即设备之原值；

　　 $C j$ ——在n年使用期间的第j年度设备的运营成本；

　　 $L n$ ——设备在第n年的净残值。

　　由上式可知，设备的年等额总成本 $A C n$ 等于设备的年等额资产恢复成本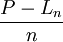 $\frac{P-L_n}{n}$ 与设备的年等额运营成本 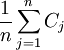$\frac{1}{n}\sum_{j=1}^n C_j$ 之和。

　　在所有的设备使用期限中，能使设备年等额总成本 $A C n$ 最低的那个使用期限就是设备的经济寿命。如果设备的经济寿命为m年，则m应满足如下不等式条件：

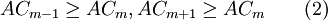
　　 $AC_{m-1}\geq AC_m,AC_{m+1}\geq AC_m \qquad (2)$

　　上式的关系也可通过图表示。

　　【例1】某型号轿车购置费为3万元，在使用中有如表1的统计资料，如果不考虑资金的时间价值，试计算其经济寿命。

　　表1 某型号轿车使用过程统计数据表单位：元

使用年度j	1	2	3	4	5	6	7
j年度运营成本	5000	6000	7000	9000	11500	14000	17000
n年末残值	15000	7500	3750	1875	1000	1000	1000

　　【解】根据公式(1)计算，该型轿车在不同使用期限的年等额总成本如表2所示。

　　表2 某型号轿车年等额总成本计算表单位：元

使用期限n	资产恢复成本 $P - L n$	年等额资产恢复成本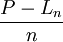 $\frac{P-L_n}{n}$	年度运营成本 $C j$	使用期限内运营成本累计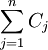 $\sum_{j=1}^n C_j$	年等额运营成本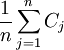 $\frac{1}{n}\sum_{j=1}^n C_j$	年等额总成本⑦=③+⑥
①	②	③	④	⑤	⑥	⑦
1	15000	15000	5000	5000	5000	20000
2	22500	11250	6000	11000	5500	16750
3	26250	8750	7000	18000	6000	14750
4	28125	7031	9000	27000	6750	13781
$5 *$	29000	5800	11500	38500	7700	$13500 *$
6	29000	4833	14000	52500	8750	13583
7	29000	4143	17000	69500	9929	14072

　　“*”表示轿车经济寿命对应的年等额总成本。

　　由计算结果来看，该型号轿车使用5年时，其年等额总成本最低( $A C 5 = 13500$ 元)，使用期限大于或小于5年时，其年等额总成本均大于13500元，故该汽车的经济寿命为5年。

　　设备的运营成本包括：能源费、保养费、修理费、停工损失、废次品损失等等。一般而言，随着设备使用期限的增加，年运营成本每年以某种速度在递增，这种运营成本的逐年递增称为设备的劣化。现假定每年运营成本的增量是均等的，即经营成本呈线性增长，如图2的现金流量所示。假定运营成本均发生在年末，设每年运营成本增加额为 $λ$ ，若设备使用期限为n年，则第n年时的运营成本为：

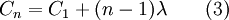
　　 $C_n=C_1+(n-1)\lambda \qquad (3)$

　　式中

　　 $C 1$ ——运营成本的初始值，即第1年的运营成本；

　　n——设备使用年限。

　　n年内设备运营成本的平均值为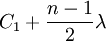： $C_1+\frac{n-1}{2}\lambda$ 。

　　除运营成本外，在年等额总成本中还包括设备的年等额资产恢复成本，其金额为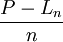 $\frac{P-L_n}{n}$ ，则年等额总成本的计算公式为：

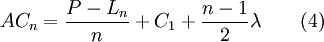
　　 $AC_n=\frac{P-L_n}{n}+C_1+\frac{n-1}{2}\lambda \qquad (4)$

　　通过求式(4)的极值，可找出设备的经济寿命计算公式。

　　设 $L n$ 为一常数，令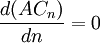 $\frac{d(AC_n)}{dn}=0$ ，则经济寿命m为：

　　 $m=\sqrt{\frac{2(P-L_n)}{\lambda}} \qquad (5)$

　　【例2】设有一台设备，购置费为8000元，预计残值800元，运营成本初始值为600元，年运营成本每年增长300元，求该设备的经济寿命。

　　【解】由式(5)可得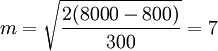： $m=\sqrt{\frac{2(8000-800)}{300}}=7$ (年)

　　2．经济寿命的动态计算方法

　　当利率不为零时，计算经济寿命需考虑资金的时间价值。按照图2所示的现金流量图，设备在n年内的等额年总成本AC。可按下式计算：

　　 $AC_n=P(A/P,i,n)-L_n(A/F,i,n)+C_1+\lambda(A/G,i,n)=[(P-L_n)(A/P,i,n)+L_n\times i]+[C_1+\lambda(A/G,i,n)] \qquad (6)$

　　式中符号同前，其中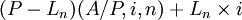 $(P-L_n)(A/P,i,n)+L_n\times i$ 为等额年资产恢复成本， $C 1 + λ(A / G, i, n)$ 为等额年运营成本。

　　等额年总成本AG更为一般的计算式如下：

　　 $AC_n=TC(A/P,i,n)=[P-L_n(P/F,i,n)+\sum_{j=1}^n C_j(P/F,i,j)](A/P,i,n) \qquad (7)$

　　式中

　　 $T C n$ ——设备在n年内的总成本现值。

　　【例3】某设备购置费为24000元，第1年的设备运营费为8000元，以后每年增加5600元，设备逐年减少的残值如表3所示。设利率为12%，求该设备的经济寿命。

　　【解】根据公式(6)，设备在使用年限内的等额年总成本计算如下：

　　n=1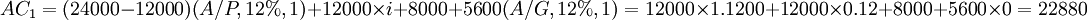： $AC_1=(24000-12000)(A/P,12%,1)+12000\times i+8000+5600(A/G,12%,1)=12000\times 1.1200+12000\times 0.12+8000+5600\times 0=22880$ (元)

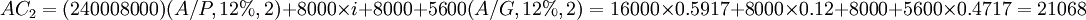　　n=2： $AC_2=(240008000)(A/P,12%,2)+8000\times i+8000+5600(A/G,12%,2)=16000\times 0.5917+8000\times 0.12+8000+5600\times 0.4717=21068$ (元)

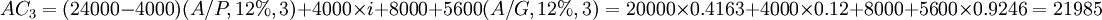　　n=3： $AC_3=(24000-4000)(A/P,12%,3)+4000\times i+8000+5600(A/G,12%,3)=20000\times 0.4163+4000\times 0.12+8000+5600\times 0.9246=21985$ (元)

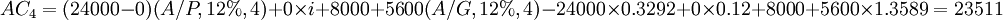　　n=4： $AC_4=(24000-0)(A/P,12%,4)+0\times i+8000+5600(A/G,12%,4)-24000\times 0.3292+0\times 0.12+8000+5600\times 1.3589=23511$ (元)

　　表3 设备经济寿命动态计算表单位：元

第j年末	设备使用到第n年末的残值	年度运营成本	等额年资产恢复成本	等额年运营成本	等额年总成本
1	12000	8000	14880	8000	22880
2	8000	13600	10427	10641	21068
3	4000	19200	8806	13179	21985
4	0	24800	7901	15610	23511

　　根据表3的计算结果，设备的经济寿命为2年。

[编辑]

参考文献

↑ 史本山，李海波，张震宇.投资经济学.西南交通大学出版社,2010.08
↑ 刘晓君主编.工程经济学.中国建筑工业出版社,2008.1

来自"https://wiki.mbalib.com/wiki/%E8%AE%BE%E5%A4%87%E7%BB%8F%E6%B5%8E%E5%AF%BF%E5%91%BD"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

郭亚龙,HEHE林,苏青荇.

页面分类: 设备管理

评论(共0条)

提示:评论内容为网友针对条目"设备经济寿命"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

设备经济寿命

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是设备经济寿命

设备经济寿命的确定^[2]

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

查看

工具箱▼

设备经济寿命

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么是设备经济寿命

设备经济寿命的确定[2]

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共0条)

导航

意见反馈

设备经济寿命的确定^[2]