统计地图
出自 MBA智库百科(https://wiki.mbalib.com/)
统计地图(Statistical Map)
目录 |
统计地图是运用统计数据反映制图对象数量特征的一种图型。可形象地反映、揭示统计项目和同一项目内不同统计标准间的同一性和差异性,以分析它们在自然和社会经济现象中的分布特征。主要表现各种社会经济现象的特征、规模、水平、结构、地理分布、相互依存关系及其发展趋势。
目前统计地图广泛应用于人口、工业、农业等各种社会经济部门,并采用计算机辅助制图方法。世界上不少国家首先发展了统计制图的软件系统,如symap系统、geomap系统、cart系统等。它们的功能一般包括统计资料的选取,统计数据的处理、分级以及图形输出等部分。
统计地图,包括分级统计图、图表统计图、定位统计图。
1、分级统计地图
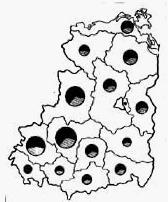
分级统计地图是按行政区划或经济区划,以不同深浅的颜色或疏密不等的晕线表示现象相对指标差异的图件(图1)。分级统计地图是等值区域制图中使用最广泛的一种形式。其原始数据是比率量表的形式,为了某种需要把它处理成间隔量表的形式。
分级可用等差、等比、标准差或任意分级方法,统称分级比值法。它只表示各统计单位之间差异,而不反映统计单位内部的差别。统计单位愈大,表示现象分布的程度就愈概略;统计单位愈小,显示的现象分布就愈接近实际。
1)分级数目
分级数目主要取决于读者阅读能力能够辨认的等级数。单色地图3~5级,多色地图7~9级。在选择分级数时,还要看区域单元的数量和数据的分布特征,只是一般不要超过上述级别。
2)分级方法
A、固定系列或等梯度
最简单的分级方法是等梯度的固有系列,即找出数据集中的最高值和最低值,将二者之差被拟定的分级数去除,得到每一级的级差,按此级差构成的分级序列。
第二种固定系列是利用一个正态分布参数来构成的,即对一个数据集求其平均数X和标准差S,以平均值为中心加减差若干标准差即构成分级数列的界限。
第三种固定系列称为嵌套平均值。其基本方法是先用总平均值将原始数列分成两部分,再求每部分的平均值将其各自又分为两部分,再求每部分的平均值将其各自又分为两部分依此类推,达到需要的级数,各平均值即为分界极限。
B、分级间隔有系统的朝量表的高端或低端变小
根据数据的分布状态,如低端包括的单元数较多,则把低端的间隔变小,反之亦然。可以采用下面的6种方式之一:
- 按某一恒定速率递增
- 按某一加速度递增
- 按某一减速度递增
- 按某一恒定速率递减
- 按某一加速度递减
- 按某一减速度递减
若采用算术级数,其增减速度是稳定的;若采用几何级数,就会造成加速或减速。
C、不规则的梯级的分级界限
不规则的梯级分级是根据每一级中包含的单元数由制图者制定分级界限,既有意识的将低端的单元数多一些,然后逐渐减少,也可以掌握使中间的单元数多一些,两端都比较少,其分级界限不一定遵循变化的固定规则。
2、图表统计地图
以图表、图形显示各统计单位内现象的总和以及内部结构的图件(图2 )。
3、定位统计地图
以统计图表表示相应点的特殊现象和变化规律(图3)。一般有柱状图表、曲线图表以及玫瑰图表等。