组合预测法
出自 MBA智库百科(https://wiki.mbalib.com/)
组合预测法(Combination Forecasting)
目录 |
组合预测方法是对同一个问题,采用两种以上不同预测方法的预测。它既可是几种定量方法的组合,也可是几种定性的方法的组合,但实践中更多的则是利用定性方法与定量方法的组合。组合的主要目的是综合利用各种方法所提供的信息,尽可能地提高预测精度。
比如,在经济转轨时期,很难有一个单项预测模型能对宏观经济频繁波动的现实拟合的非常紧密并对其变动的原因作出稳定一致的解释。理论和实践研究都表明,在诸种单项预测模型各异且数据来源不同的情况下,组合预测模型可能导致一个比任何一个独立预测值更好的预测值,组合预测模型能减少预测的系统误差,显著改进预测效果[1]。
组合预测有两种基本形式:
1、等权组合,即各预测方法的预测值按相同的权数组合成新的预测值。
2、不等权组合,即赋予不同预测方法的预测值的权数是不一样的。
这两种形式的原理和运用方法完全相同,只是权数的取定上有所区别。根据已进行的预测结果,采用不等权组合的组合预测法结果较为准确。
组合预测法的原则及步骤[1]
组合预测法的应用原则以及一般步骤
1、应用原则:定性分析与定量分析相结合原则;系统性原则;经济性原则。
2、步骤:以经济预测为例,一般步骤是根据经济理论和实际情况建立各种独立的单项预测模型;运用系统聚类分析方法度量各单项模型的类间相似程度;根据聚类结果,逐层次建立组合预测模型进行预测。
组合预测模型模式一:线性组合模型;模式二:最优线性组合模型;模式三:贝叶斯组合模型;模式四:转换函数组合模型;模式五:计量经济与系统动力学组合模型。
案例一:组合预测法分析绿色纺织品的市场销量[2]
一、绿色纺织品的国际地位
目前,全球纺织品和服装的年交易总额约为4000亿美元(仅次于旅游产业和信息产业,名列第三),我国占全球纺织品和服装年交易总额的1/8,约500亿美元& 中国已连续) 年保持世界最大的纺织品生产国和出口国地位,纺织品年出口额占中国出口商品总量的(30%左右,在美、欧、日所占市场份额分别是15%、15.2%和59.4%“入世”给我国纺织品出口带来了机遇,纺织品出口配额将被取消,关税降低,进口的棉花和其他辅料关税的下降,有利于降低纺织品生产成本,增加市场竞争力。但当前以欧、美为代表的发达国家所构筑的“绿色贸易壁垒”已成为一种新型的非关税壁垒形式,并将成为限制我国纺织品出口的重要因素1998年某企业有一批价值100万美元纺织品出口欧洲受阻,原因是检测时发现布料染料中的化学成分对人体有害[3]。2002年某厂生产的30余万件夹克从欧洲被退回,理由是服装拉锁的有关金属含量超过了欧洲标准,诸如此类例子不胜枚举,绿色纺织品已成为国际市场的流行趋势,不但广受消费者的欢迎,也已成为发达国家构筑非关税壁垒,限制纺织品进口的新手段,企业如能更新观念,研究进口国有关环保法规及相关的产品标准,生产绿色纺织品,不但能帮助企业跨过绿色贸易壁垒,还能帮助企业扩大出口量。[4]尝试利用组合预测法分析影响绿色纺织品的市场销量的主要因素,预测其市场销量与发展前景。
二、组合预测法
例:我国某纺织企业为其某品牌的绿色纺织品进入欧洲某国的市场销量进行预测! 该企业的国际销售部除自行调查预测外,还委托目标市场国的两家市场调研公司进行调查预测,分别得出三种不同的预测模型:
(1)Y1 = 5.1 + 0.0046X1 + 12.35X1
(2)Y2 = 8.845 + 3.234X3
(3)Y3 = 3.693 − 5.62X4 + 4.74X5
Yi—— 目标市场国的月销量;
X1—— 目标市场国的人均月收入;
X1—— 目标市场国的绿色消费者比例;
X4—— 每月绿色广告费用;
C—— 本公司绿色纺织品价格;
X5—— 目标市场国主要竞争对手的绿色纺织品价格。
三个预测主体根据其独自掌握的信息,加上大家所共享的信息,分别选择了最合适的方法对绿色纺织品的销量进行预测,拟合出不同的最优预测模型。显然,这些预测结果各不相同,甚至差距很大,但我们可综合各种预测结果,进行组合优化,来分析绿色纺织品的销量。
1.期望值法
对得出的各种预测结果计算加权算术平均数,即
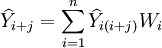
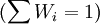
权数Wi有不同的取值方法,较常用的有:
- 等权法
取 当各种预测结果较为集中,且各种预测技术在各自信息数据条件下皆为最优模型时采用
当各种预测结果较为集中,且各种预测技术在各自信息数据条件下皆为最优模型时采用
- 拟合优度法
取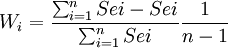
式中Sei——第i个预测模型标准误差
当各种预测结果较分散,该模型能予以预测标准误差最小的模型以最大的权重,使预测结果保证拟合优度
- 正态分布法
取Wi = Ci − 1 − n − 1 / 2n − 1 式中C——组合符号
当各种预测结果排列近似于对称分布时,该方法使组合预测结果趋近众多预测结果的中位数
- 组合中心法
取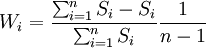 其中
其中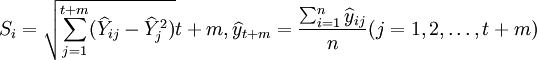
式中Si—— 第i种模型的预测结果与各种模型预测结果的均值的离差平方平均数的二次方根;
n—— 预测模型的个数;t—— 用于拟合模型的已知数据个数;
m—— 模型拟就以后所得数据的顺序。
该法给予预测结果与等权组合预测结果最接近的模型以最大的权重
- 交集法
当各种预测结果为区间预测时,可取各种预测模型同一置信区间的相交区域作为组合预测的置信区间,并根据各种情况做相应处理。当各种预测结果为点预测时,组合预测置信区间通常采用第一四分位数至第三四分位数
三、组合预测法分析绿色纺织品的市场销量
该企业以三个模型为基础进行组合预测。已知:
X1 = 2400美元,X2 = 61%,X3 = 5万美元,X4 = 23美元,X5 = 31美元。计算得Y1 = 23.6335,Y2 = 25.015,Y3 = 21.373。分别利用各种组合技术预测绿色纺织品的市场销量
1.等权预测
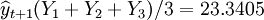 (万件)
(万件)
2.拟合优度预测
已知:三种模型的标准误分别为1.417,2.149,2.338.先计算权数得
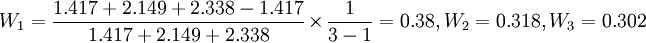
于是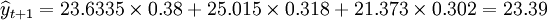 (万件)
(万件)
3.正态分布预测
先计算权数得W_1=C^{1-1}_{3-1}/2^{3-1}=0.25,W_2=C^{2-1}_{3-1}/2^{3-1}=0.50,W_3=C^{3-1}_{3-1}/2^{3-1}=0.25
于是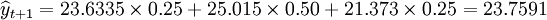 (万件)
(万件)
4.组合中心预测
已知: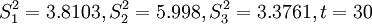
先求t+1中的Si,得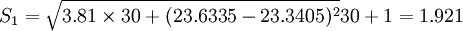 ,
,
S2 = 2.428,S3 = 1.8418
再求权数,得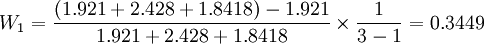 ,
,
W2 = 0.3039,W3 = 0.3512
于是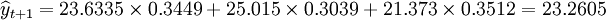 (万件)
(万件)
5.置信区间重叠预测
设取置信区间为95%,则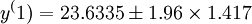
即20.8562~26.4108
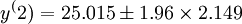
即20.703~29.227
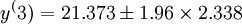
即16.7905~25.9555
于是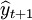 的95%的置信区间为25.955(万件)
的95%的置信区间为25.955(万件)
因此,国内纺织企业今后应加强绿色纺织品的研究,不但要提高产品质量,而且要做到知己知彼,了解目标市场国对绿色纺织品的需求,进行市场调研与预测+ 在市场调研与预测过程中要注意以下几点:
(1)影响市场销量的因素有很多,在取绿色价格、人均月收入、绿色消费者的比例、竞争对手的绿色价格为自变量拟合了三个简单的多元线性回归模型。现实调研中,企业往往由于经费的限制或简单的仅以低价取胜为原则,设立的模型过于简单,调研结果达不到理想的效果
(2)单个模型预测往往达不到理想的效果,如本文的案例中虽有三个多元线性回归模型,但分别为三个预测主体设立,过于简单+ 解决的办法是拟合联立方程组模型来较单个方程模型更全面地描述市场现象,以求更理想的预测效果,如可以考虑设立如下方程组:
生产成本=F(生产量、广告费用、其他销售费用)
价格=F(生产成本、普及率、市场竞争)
普及率=F(以前的销售量、人均收入水平)
广告费用=F(销售量、市场竞争)
案例二:组合预测法在物流需求中的应用[5]
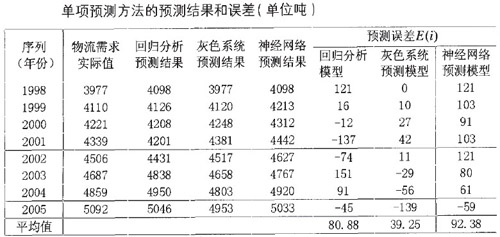
选取某物流公司物流需求量的历史数据序列,取1998-2005年的数据为样本,用Y1、Y2、Y3。分别代表回归分析、灰色系统、神经网络3种不同的预测模型对物流需求进行预测,并将三种预测模型的结果与实际值进行比较计算预测误差如表所示:
通过比较上述三种模型预测误差绝对值的平均值,可以看到在本次物流需求中,神经网络的误差最大,回归分析次之,灰色模型预测的误差最小,这正反映了各种模型在物流需求预测中的优缺点。按照上表的计算结果可得组合预测的总误差为E=\frac{1}{3}(80.88+39.25+92.38)=70.84
根据Shapley值得概念,参与组合预测模型总误差分摊的“合作关系”的成员为:N={1,2,3},它的所有子集的组合的误差值分别为它的所有子集的组合的误差值分别为E{1}、E{2}、E{3}、E{1,2}、E{1,3}、E{2,3}E{1,2,3},其数值的大小为该子集所包括向量误差的均值大小如表2所示
表各子集的误差值
| E{1} | E{2} | E{3} | E{1,2} | E{1,3} | E{2,3} | E{1,2,3} |
| 80.88 | 39.25 | 92.38 | 60.06 | 86.63 | 65.82 | 70.84 |
按照公式(3),(4)的Shapley值计算方法,求各成员的Shapley值为:
![E_1=\frac{0!2!}{3!}\left[E{1}-E({1}1})\right]+\frac{1!1!}{3!}\left[E{1,2E({1,2}1})\right]+\frac{1!1!}{3!}\left[E{1,3E({1,3}1})\right]+\frac{2!0!}{3!}\left[E{1,2,3E({1,2,3}1})\right]=31.14](/w/images/math/d/1/7/d17edd90a96824c7d3dca0e14bffd12a.png)
同样可得单项预测方法y_2,y_3应当分摊的误差量为:E2 = − 0.07,E3 = 39.77。而E1 + E2 + E3 = 70.84说明三种单一预测方法分摊的误差的和等于总的误差量E,即各个方法分摊误差的计算结果正确。各分摊值的大小则说明了各自预测模型的精度的大小。根据上面的计算结果和公式(5),计算各个预测方法在组合模型中的最终的权重为:
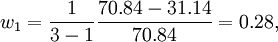
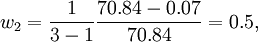
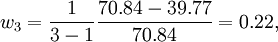
根据所得的组合权重我们可知组合预测模型为:Y=O.28+0.5+0.22。Y为组合预测模型的预测值。利用组合预测模型Y对1998-2005进行物流需求预测,并计算组合预测结果的误差及相对误差如下表所示:
表物流需求组合预测值及误差、相对误差
| 年份序列 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| 物流需求实际值 | 3977 | 4110 | 4221 | 4339 | 4506 | 4687 | 4859 | 5092 |
| 组合预测值 | 4037.5 | 4142.1 | 4250.9 | 4344.0 | 4517.1 | 4732.3 | 4869.9 | 4996.6 |
| 组合预测误差 | 60.5 | 32.1 | 29.9 | 5.0 | 11.1 | 45.3 | 10.9 | -95.3 |
| 组合预测相对误差(%) | 1.52 | 0.78 | 0.7l | O.12 | 0.25 | 0.97 | 0.23 | -1.87 |
从上表可知:基于Shapley值法的权重分配组合预测方法模型在物流需求预测的应用中具有较好的预测能力,大部分组合预测的相对误差保持在1%之内,只有1998,2005年的相对误差超过这个范围,但也未超过2%。
可看出该权重分配法的组合预测方法在物流需求预测中能很好的达到物流需求预测的要求,并且计算过程简单,对数学基础要求不高,值得推广应用。








例子中的拟合优度法的标准误差怎么求呢?