灰色系统预测法
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
灰色系统预测法是指对一些行为效果已知、而产生行为的原因较模糊的抽象灰色系统的预测方法。所谓灰色系统是介于白色系统和黑箱系统之间的过渡系统,一般地说,社会系统、经济系统、生态系统都是灰色系统。
灰色系统预测主要包括:
1.数列预测,即对系统行为特征值的预测。
2.激励预测,即对在一些突然性因素影响下的行为特征值的预测。
3.突变预测,即对系统的行为特征值超过一定限度而造成“突变”的时间的预测。
4.季节突变预测,即在某一特定时期内发生的突变的预测。
5.拓展预测,是对不规则波动系统的行为特征的波形的预测。
6.系统预测,是一种综合预测,即先用不同模型表示变量之间的关系,得到一组模型,然后再进一步采用模型来表示诸模型组之间的关系,得到一个复合模型来进行预测。
该预测方法具有以下特点:
- 不需要大量的样本;
- 预测精度较高;
- 用累加生成拟合微分方程,符合能量系统的变化规律;
- 可以进行长期预测。
(1)数据处理。假设给定原始时间数据序列为:
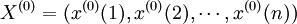 (4-40)
(4-40)
这些数据表现为:量少、无规律、随机性强、波动明显等。此时,将原始数据列进行一次累加生成1-AGO,获得新的数据列:
 (4-41)
(4-41)
式中,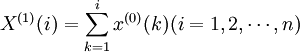 。由于新生成的数据列为一条单调增长的曲线,增加了原始数据列的规律性,弱化了其波动性。
。由于新生成的数据列为一条单调增长的曲线,增加了原始数据列的规律性,弱化了其波动性。
(2)建立微分方程。灰色系统建模思想是直接将时间序列转化为微分方程,从而建立抽象系统的发展变化动态模型,简记为GM。GM(1,1)模型的原始形式为:x(0)(k) + ax(1)(k) = b,其中,G表示Grey,M表示Model,1表示1阶方程,1表示1个变量,a和b为参数。设
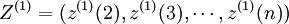 (4-42)
(4-42)
式中,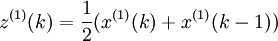 ,则称
,则称
x(0)(k) + az(1)(k) = b (4-43)
为GM(1,1)模型的基本形式。
若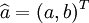 为参数列,且
为参数列,且
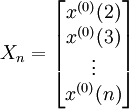 ,
,
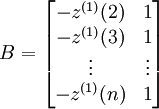 (4-44)
(4-44)
则灰色微分方程式(4-44)的最小二乘估计参数列满足:
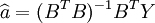 (4-45)
(4-45)
设非负序列X(0)和1-AGO序列X(1)如式(4-41)和式(4-42)所示,其中Z(1)为X(1)的紧邻均值生成序列,如式(4-43)所示,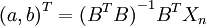 ,
,
则称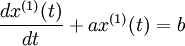 (4-46)
(4-46)
为灰色微分方程式(4-44)的白化方程,也叫影响方程。进行物流预测时,常常采用该白化方程。
(3)参数估计a和b。具体公式为式(4-45)和式(4-46),其中式(4-45)结合式(4-43)代入得
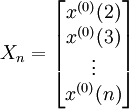 ,
,
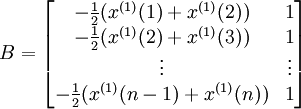 (4-47)
(4-47)
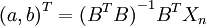 (4-48)
(4-48)
把式(4-47)代入式(4-48)可得a和b的值。
(4)预测模型。白化方程式(4-46)的解也称时间相应预测值,具体为:
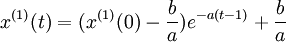 (4-49)
(4-49)
GM(1,1)灰色微分方程式(4-43)或式(4-46)的时间相应序列为:
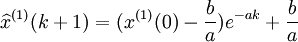 ,
,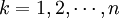 (4-50)
(4-50)
取x(1)(0) = x(0)(1),则
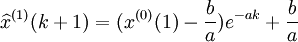 ,
,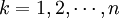 (4-51)
(4-51)
(5)还原模型。最后由于灰色系统理论建立的是累加数据的模型,因此我们必须对累加的数据进行还原,得到还原模型:
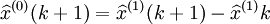 ,
,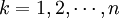 (4-52)
(4-52)
GM(1,1)模型的综合预测模型为:
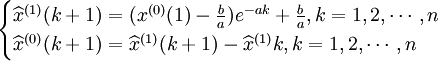
设原始序列为式(4-41),相应的预测模型序列为:
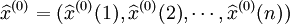
残差序列为:
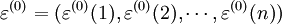
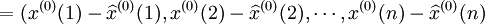
(1)残差检验。按预测模型计算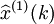 ,并将
,并将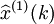 累减生成
累减生成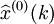 ,然后计算原始数据x(0)(k)与预测值
,然后计算原始数据x(0)(k)与预测值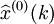 的绝对误差序列和相对误差序列:
的绝对误差序列和相对误差序列:
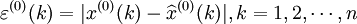 (4-53)
(4-53)
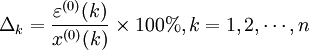 (4-54)
(4-54)
对于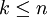 ,称
,称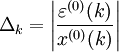 为k点模拟相对误差,称
为k点模拟相对误差,称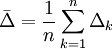 为平均相对误差;称
为平均相对误差;称 为平均相对精度,1 − Δk为k点的模拟精度
为平均相对精度,1 − Δk为k点的模拟精度 。给定α,当Δ < α且Δk < α成立时,该模型为残差合格模型。
。给定α,当Δ < α且Δk < α成立时,该模型为残差合格模型。
(2)后验差检验。第1后验指标为方差比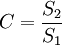 ,对于给定的C0 > 0,当C < C0时,称模型为均方差合格模型。第2后验指标为小误差概率
,对于给定的C0 > 0,当C < C0时,称模型为均方差合格模型。第2后验指标为小误差概率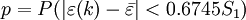 ,对于给定的p0 > 0,当p < p0时,称模型为小误差概率合格模型。
,对于给定的p0 > 0,当p < p0时,称模型为小误差概率合格模型。
上述式中:S1位原始序列标准差;S2为绝对误差标准差;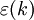 为预测误差;
为预测误差;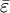 为其均值;p=m/n(m为小于上述条件的误差个数)。通过检验的标准为精度等级月消越好,4级为不通过,精度等级如表4-8所示。
为其均值;p=m/n(m为小于上述条件的误差个数)。通过检验的标准为精度等级月消越好,4级为不通过,精度等级如表4-8所示。
| 精度等级 | ||||
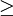 0.20 0.20
| ||||
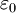 | 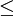 0.60 0.60
| |||
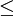 0.70 0.70
| ||||
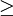 0.65 0.65
| ||||
虽然GM(1,1)模型在预测方面应用广泛且效果显著,但并不是所有的数据序列都能建立GM(1,1)模型。在建立GM(1,1)模型之前,数列必须满足一定的前提条件:
1)数据序列要满足准光滑性条件,光滑比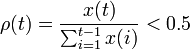 为准光滑性检验条件;
为准光滑性检验条件;
2)数据序列必须满足灰指数规律,序列的变化速度不能太快,级比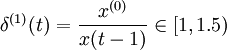 为准指数规律检验条件。
为准指数规律检验条件。
对于满足准光滑性条件和灰指数规律的序列,可以建立GM(1,1)模型。一般非负系列累加生成后,可以得到光滑序列,非负光滑序列累加生成后,都会减少随机性,呈现出近似的指数增长规律。原始数列越光滑,生成后的指数规律也越明显。因此保证数列光滑性是生成指数的关键。对于非光滑或震荡数列,一般经过二级弱化算子作用后就能变成为光滑数列。







