激励相容约束
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
- 激励相容约束(Incentive Compatibility Constraint)
目录 |
[编辑]
什么是激励相容约束[1]
激励相容约束是指在一个激励合同下，代理人总是在所有可能的行动集中选择能使自己期望效用最大化的行动。
[编辑]
激励相容约束的不成立[2]
激励相容约束不成立，这种情况可以描述为：代理人（或者工程师）有权利决定是否接受委托人（或者业主）的委托，但是一旦接受，工程师的积极性得不到尊重和保障，即业主只关心工程师是否愿意接受合同，而对工程师接受合同之后是否愿意努力工作不予关心。我国的工程监理在不同程度上存在这些情况，如监理取费固定、工程实行监理仅仅是用于应付检查和规章制度等。下面分析这种情况下委托-代理双方的行为及收益。
委托—代理模型如下： maxα,β,aEv = − α + (1 − β)a
s.t.=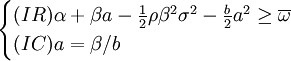
将上述公式进行一系列的变形得到：
公式一：
公式二：
对上式中的a、β求导并令之为0，得β = 0,
。
将a、β再代入公式一，可得
同样将β代入公式二，可得
以上结果可以看到，在这种情况下(β = 0)，即业主只支付给工程师固定报酬，工程师是否努力工作从报酬上看是没有区别的。由此考虑到付出努力带来的成本，工程师从最大化自己收益的角度出发，将会选择最优努力为0。由于工程师不付出努力，业主的收益为
，即白白为工程师支付了满足参与约束所需的最低报酬，而业主雇佣工程师的目的没有实现。
[编辑]
