极值定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
在微积分中，极值定理是指如果实函数f在闭区间[a,b]上是连续函数，则它一定取得最大值和最小值，至少一次。也就是说，存在[a,b]内的c和d，使得：
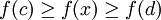对于所有![x\in [a,b]](/w/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png)
。
一个相关的定理是有界性定理，它说明闭区间[a,b]内的连续函数f在该区间上有界。也就是说，存在实数m和M，使得：
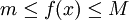对于所有。
极值定理强化了有界性定理，它表明函数不仅是有界的，而且它的最小上界就是最大值，最大下界就是最小值。
我们来证明f的上界和最大值的存在。把这个结果应用于函数–f，也可推出f的下界和最小值的存在。
我们首先证明有界性定理，它是证明极值定理中的一个步骤。证明极值定理的基本步骤为：
证明有界性定理。
寻找一个序列，它的像收敛于f的最小上界。
证明存在一个子序列，它收敛于定义域内的一个点。
用连续性来证明子序列的像收敛于最小上界。
假设函数f在区间[a,b]内连续且没有上界。那么，根据实数的阿基米得公理，对于每一个自然数n，都存在[a,b]内的一个xn，使得f(xn) > n。这便定义了一个序列{xn}。由于[a,b]是有界的，根据波尔查诺-魏尔施特拉斯定理，可推出存在{xn}的一个收敛的子序列{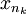
}。把它的极限记为x。由于[a,b]是闭区间，它一定含有x。因为f在x处连续，我们知道{f(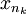)}收敛于实数f(x)。但对于所有的k，都有f(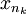) > nk ≥ k，这意味着{f(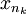)}发散于无穷大。得出矛盾。因此，f在[a,b]内有上界。证毕。
根据有界性定理，f有上界，因此，根据实数的戴德金完备性，f的最小上界M存在。我们需要寻找[a,b]内的一个d，使得M = f(d)。设n为一个自然数。由于M是最小上界，M – 1/n就不是f的最小上界。因此，存在[a,b]内的dn，使得M – 1/n < f(dn)。这便定义了一个序列{dn}。由于M是f的一个上界，我们便有M – 1/n < f(dn) ≤ M，对于所有的n。因此，序列{f(dn)}收敛于M。
根据波尔查诺-魏尔施特拉斯定理，可知存在一个子序列{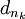
}，它收敛于某个d，且由于[a,b]是闭区间，d位于[a,b]内。因为f在d处连续，所以序列{f(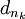)}收敛于f(d)。但{f(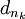)}是{f(dn)}的一个子序列，收敛于M，因此M = f(d)。所以，f在d处取得最小上界M。证毕。
以下的例子说明了为什么函数的定义域需要是封闭和有界的。
定义在[0,∞)的函数f(x) = x没有上界。
定义在[0,∞)的函数f(x) = x/(1 + x)有界，但不取得最小上界1。
定义在(0,1]的函数f(x) = 1/x没有上界。
定义在(0,1]的函数f(x) = 1 –x有界，但不取得最小上界1。
如果把f的连续性减弱为半连续，则有界性定理和极值定理的对应的一半仍然成立，且扩展的实数轴上的值–∞和+∞也可以允许为可能的值。更加精确地：
定理：如果函数f : [a,b] → [–∞,∞)是上半连续的，也就是说，对于[a,b]内的所有x，都有：
，
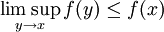那么f有上界，且取得最小上界。
证明：如果对于[a,b]内的所有x，都有f(x) = –∞，那么最小上界也是–∞，于是定理成立。在任何其它情况下，只需把上面的证明稍加修改便可。在有界性定理的证明中，f在x处的半连续性只意味着子序列{f(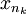)}的上极限有上界f(x) < ∞，但这已足以得到矛盾。在极值定理的证明中，f在d处的半连续性意味着子序列{f(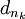)}的上极限有上界f(d)，但这已足以推出f(d) = M的结论。证毕。
把这个结果应用于−f，可得：
定理：如果函数f : [a,b] → (–∞,∞]是下半连续的，也就是说，对于[a,b]内的所有x，都有：
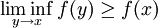
那么f有下界，且取得最大下界。
一个实函数是上半连续且下半连续的，当且仅当它是连续的。因此，从这两个定理就可以推出有界性定理和极值定理。
函数的极值不仅是反映函数性态的一个重要特征，而且在解决实际问题中也占有极其重要的地位。很多经济和生活中的问题都可以转化为数学中的函数极值问题进行讨论，从而得到该问题的最优方案。
