極值定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
在微積分中，極值定理是指如果實函數f在閉區間[a,b]上是連續函數，則它一定取得最大值和最小值，至少一次。也就是說，存在[a,b]內的c和d，使得：
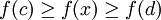對於所有![x\in [a,b]](/w/images/math/8/2/9/8290bddba5acf9822dcbf61f4ac67d1b.png)
。
一個相關的定理是有界性定理，它說明閉區間[a,b]內的連續函數f在該區間上有界。也就是說，存在實數m和M，使得：
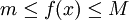對於所有。
極值定理強化了有界性定理，它表明函數不僅是有界的，而且它的最小上界就是最大值，最大下界就是最小值。
我們來證明f的上界和最大值的存在。把這個結果應用於函數–f，也可推出f的下界和最小值的存在。
我們首先證明有界性定理，它是證明極值定理中的一個步驟。證明極值定理的基本步驟為：
證明有界性定理。
尋找一個序列，它的像收斂於f的最小上界。
證明存在一個子序列，它收斂於定義域內的一個點。
用連續性來證明子序列的像收斂於最小上界。
假設函數f在區間[a,b]內連續且沒有上界。那麼，根據實數的阿基米得公理，對於每一個自然數n，都存在[a,b]內的一個xn，使得f(xn) > n。這便定義了一個序列{xn}。由於[a,b]是有界的，根據波爾查諾-魏爾施特拉斯定理，可推出存在{xn}的一個收斂的子序列{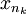
}。把它的極限記為x。由於[a,b]是閉區間，它一定含有x。因為f在x處連續，我們知道{f(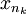)}收斂於實數f(x)。但對於所有的k，都有f(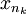) > nk ≥ k，這意味著{f(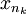)}發散於無窮大。得出矛盾。因此，f在[a,b]內有上界。證畢。
根據有界性定理，f有上界，因此，根據實數的戴德金完備性，f的最小上界M存在。我們需要尋找[a,b]內的一個d，使得M = f(d)。設n為一個自然數。由於M是最小上界，M – 1/n就不是f的最小上界。因此，存在[a,b]內的dn，使得M – 1/n < f(dn)。這便定義了一個序列{dn}。由於M是f的一個上界，我們便有M – 1/n < f(dn) ≤ M，對於所有的n。因此，序列{f(dn)}收斂於M。
根據波爾查諾-魏爾施特拉斯定理，可知存在一個子序列{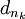
}，它收斂於某個d，且由於[a,b]是閉區間，d位於[a,b]內。因為f在d處連續，所以序列{f(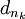)}收斂於f(d)。但{f(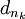)}是{f(dn)}的一個子序列，收斂於M，因此M = f(d)。所以，f在d處取得最小上界M。證畢。
以下的例子說明瞭為什麼函數的定義域需要是封閉和有界的。
定義在[0,∞)的函數f(x) = x沒有上界。
定義在[0,∞)的函數f(x) = x/(1 + x)有界，但不取得最小上界1。
定義在(0,1]的函數f(x) = 1/x沒有上界。
定義在(0,1]的函數f(x) = 1 –x有界，但不取得最小上界1。
如果把f的連續性減弱為半連續，則有界性定理和極值定理的對應的一半仍然成立，且擴展的實數軸上的值–∞和+∞也可以允許為可能的值。更加精確地：
定理：如果函數f : [a,b] → [–∞,∞)是上半連續的，也就是說，對於[a,b]內的所有x，都有：
，
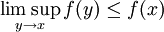那麼f有上界，且取得最小上界。
證明：如果對於[a,b]內的所有x，都有f(x) = –∞，那麼最小上界也是–∞，於是定理成立。在任何其它情況下，只需把上面的證明稍加修改便可。在有界性定理的證明中，f在x處的半連續性只意味著子序列{f(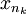)}的上極限有上界f(x) < ∞，但這已足以得到矛盾。在極值定理的證明中，f在d處的半連續性意味著子序列{f(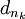)}的上極限有上界f(d)，但這已足以推出f(d) = M的結論。證畢。
把這個結果應用於−f，可得：
定理：如果函數f : [a,b] → (–∞,∞]是下半連續的，也就是說，對於[a,b]內的所有x，都有：
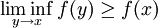
那麼f有下界，且取得最大下界。
一個實函數是上半連續且下半連續的，當且僅當它是連續的。因此，從這兩個定理就可以推出有界性定理和極值定理。
函數的極值不僅是反映函數性態的一個重要特征，而且在解決實際問題中也占有極其重要的地位。很多經濟和生活中的問題都可以轉化為數學中的函數極值問題進行討論，從而得到該問題的最優方案。
