斯蒂文斯定律

出自 MBA智库百科(https://wiki.mbalib.com/)

　　斯蒂文斯定律是指心理量S是物理量I的幂函数，用公式表示即P = KIⁿ(其中P指知觉到的大小或感觉大小；I指刺激的物理量；K和n是被评定的某类经验的常定特征，既感觉量与刺激量的乘方呈正比。即心理量并不随刺激量的对数的上升而上升，而是刺激量的乘方函数（或幂函数）。

　　20世纪中叶，史蒂文斯对费希纳的对数定律进行了批评。1957年，他根据多年的研究结果，提出了刺激强度和感觉量之间关系的斯蒂文斯定律：P = KIⁿ。 幂函数的指数值决定着按此公式所画曲线的形状。例如，当指数值为1．0时，便是一条直线，即刺激和感觉之间为简单的正比关系；指数大于1时，则为正加速曲线；小于1时，便为负加速曲线。

　　史蒂文斯用数量估计法获得了大量的实验数据。数量估计法是制作感觉比例量表的一种直接方法。具体的步骤是实验者先呈现一个标准刺激，例如一个重量（或某一明度），并规定它的出现值为一个数字，例如 1．00，然后让被试以这个主观值为标准，把其他同类强度不同的主观值，放在这个标准刺激的主观值的关系中进行判断，并用一个数字表示出来。表511就是三种感觉道所获得的实验结果。

　　根据表1的实验结果，以物理量为横坐标，以心理量为纵坐标，就可绘成图1。如果把这三个感觉道的实验结果画在双对数坐标上，就形成了三条斜率不同的直线，如图2所示。我们从图1和图2上可看到，电击的感觉强度比产生电击的物理强度的增长快得多（a＝3．5），明度比光能的增长却慢得多（a=0．34），线段的主观长度和线段的物理长度则有同样的增长率（a=1）。

　　表1 三种感觉通道的心理强度

物理量	心理量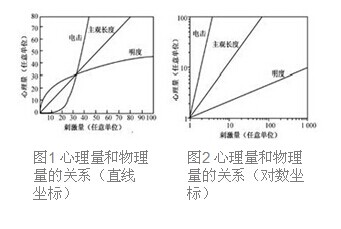
	明度	长度	电击
1	1.00	1.00	1.00
2	1.25	2.14	11.3
3	1.44	3.35	46.8
4	1.59	4.60	128
5	1.71	5.87	280
6	1.82	7.18	529
7	1.91	8.50	908
8	2.00	9.85	1450
9	2.08	11.2	2190
10	2.15	12.6	3160

　　斯蒂文斯定律并不适用于十分靠近阈限的微弱刺激。于是，史蒂文斯等人在20世纪60年代初又提出了修正的幂函数，即从刺激中减去一个常数：S=b(I,I_0) 这样，斯蒂文斯定律便可适用于全部可知觉的刺激范围。在某些研究者看来，I_0就是绝对阈限值。从I中减去I_0，意味着以阈限上有效单位而不是以物理表中零点以上单位去说明刺激的。

　　幂定律在对数定律的基础上前进了一大步。但是，幂定律的有效性有赖于被试正确使用数字去标示其真正的感觉量。那么，这里要问：不同感觉通道之间的主观量能否比较，能否调节一个感觉通道中的刺激强度使其主观上感到好像同另一感觉通道中的刺激一样强？为克服这一局限，史蒂文斯于 1959年研究了跨感觉通道的匹配技术，它无须被试产生数字等判断，被试的任务是把两个不同感觉通道产生的感觉量相等起来。例如，可以要求被试调整施加于指端的振动强度，以便使振动的感觉印象和一爆破音的响度相匹配。这样，在不同的刺激水平上获得跨感觉通道的匹配，于是一条称为等感觉函数的曲线便产生了，它可表示出一感觉通道的刺激值与造成相等感觉量判断的另一感觉通道刺激的关系。这种方法称为等感觉匹配法（equal-sensation functions obtained by matches）。